题目内容
 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( )
如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( )(1)EP⊥AC;
(2)EP∥BD;
(3)EP∥面SBD;
(4)EP⊥面SAC.
分析:如图所示,连接AC、BD相交于点O,连接EM,EN.
(1)由正四棱锥S-ABCD,可得SO⊥底面ABCD,AC⊥BD,进而得到SO⊥AC.
可得AC⊥平面SBD.由已知E,M,N分别是BC,CD,SC的中点,利用三角形的中位线可得EM∥BD,MN∥SD,于是平面EMN∥平面SBD,进而得到AC⊥平面EMN,AC⊥EP.
(2)由异面直线的定义可知:EP与BD是异面直线,因此不可能EP∥BD;
(3)由(1)可知:平面EMN∥平面SBD,可得EP∥平面SBD;
(4)由(1)同理可得:EM⊥平面SAC,可用反证法证明:当P与M不重合时,EP与平面SAC不垂直.
(1)由正四棱锥S-ABCD,可得SO⊥底面ABCD,AC⊥BD,进而得到SO⊥AC.
可得AC⊥平面SBD.由已知E,M,N分别是BC,CD,SC的中点,利用三角形的中位线可得EM∥BD,MN∥SD,于是平面EMN∥平面SBD,进而得到AC⊥平面EMN,AC⊥EP.
(2)由异面直线的定义可知:EP与BD是异面直线,因此不可能EP∥BD;
(3)由(1)可知:平面EMN∥平面SBD,可得EP∥平面SBD;
(4)由(1)同理可得:EM⊥平面SAC,可用反证法证明:当P与M不重合时,EP与平面SAC不垂直.
解答:解:如图所示,连接AC、BD相交于点O,连接EM,EN.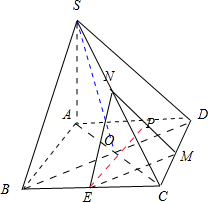
(1)由正四棱锥S-ABCD,可得SO⊥底面ABCD,AC⊥BD,∴SO⊥AC.
∵SO∩BD=O,∴AC⊥平面SBD,
∵E,M,N分别是BC,CD,SC的中点,∴EM∥BD,MN∥SD,而EM∩MN=N,
∴平面EMN∥平面SBD,∴AC⊥平面EMN,∴AC⊥EP.故正确.
(2)由异面直线的定义可知:EP与BD是异面直线,不可能EP∥BD,因此不正确;
(3)由(1)可知:平面EMN∥平面SBD,∴EP∥平面SBD,因此正确.
(4)由(1)同理可得:EM⊥平面SAC,若EP⊥平面SAC,则EP∥EM,与EP∩EM=E相矛盾,因此当P与M不重合时,EP与平面SAC不垂直.即不正确.
综上可知:只有(1)(3)正确.即四个结论中恒成立的个数是2.
故选B.

(1)由正四棱锥S-ABCD,可得SO⊥底面ABCD,AC⊥BD,∴SO⊥AC.
∵SO∩BD=O,∴AC⊥平面SBD,
∵E,M,N分别是BC,CD,SC的中点,∴EM∥BD,MN∥SD,而EM∩MN=N,
∴平面EMN∥平面SBD,∴AC⊥平面EMN,∴AC⊥EP.故正确.
(2)由异面直线的定义可知:EP与BD是异面直线,不可能EP∥BD,因此不正确;
(3)由(1)可知:平面EMN∥平面SBD,∴EP∥平面SBD,因此正确.
(4)由(1)同理可得:EM⊥平面SAC,若EP⊥平面SAC,则EP∥EM,与EP∩EM=E相矛盾,因此当P与M不重合时,EP与平面SAC不垂直.即不正确.
综上可知:只有(1)(3)正确.即四个结论中恒成立的个数是2.
故选B.
点评:熟练掌握线面、面面的位置关系判定定理是解题的关键.

练习册系列答案
相关题目
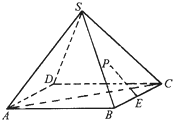 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( ) 如图,在正四棱锥S-ABCD中,AB=
如图,在正四棱锥S-ABCD中,AB= 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )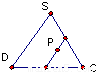
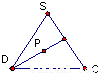
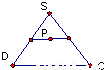
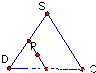
 如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )
如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE⊥AC.则动点P的轨迹与△SCD组成的相关图形是( )