题目内容
已知函数![]() ,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
(1)当t=2时,求函数f(x)的单调递增区间;
(2)设|MN|=g(t),试求函数g(t)的表达式
(3)在(2)的条件下,若对任意的正整数n,在区间[![]() ]内总存在m+1个实数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
]内总存在m+1个实数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
答案:
解析:
解析:
|
解:(1) (2)令 同理,由PN方程得 (3) 注意到 |

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
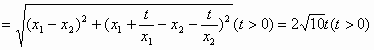 10分
10分 ,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
 内总存在m+1个数
内总存在m+1个数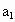 ,
, ,…,
,…, ,
, ,使得不等式
,使得不等式 成立,求m的最大值.
成立,求m的最大值.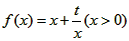 ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N,
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N,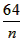 ]内,总存在m+1个数a1,a2,....,am,
]内,总存在m+1个数a1,a2,....,am,