题目内容
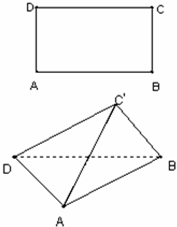
在矩形ABCD中，AB=4，BC=3，沿AC将矩形ABCD折成一个直二面角B-AC-D，则四面体ABCD的外接球的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
分析：球心到球面各点的距离相等，即可知道外接球的半径，就可以求出其体积了．
解答：解：由题意知，球心到四个顶点的距离相等，
所以球心在对角线AC上，且其半径为AC长度的一半，
则V球=
π×（
）3=
．
故选C．
所以球心在对角线AC上，且其半径为AC长度的一半，
则V球=
| 4 |
| 3 |
| 5 |
| 2 |
| 125π |
| 6 |
故选C．
点评：本题考查学生的思维意识，对球的结构和性质的运用，是基础题．
练习册系列答案
相关题目
如图，在矩形ABCD中，AB=3
如图，在矩形ABCD中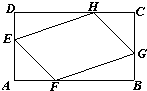，已知AD=2，AB=a（a＞2），E、F、G、H分别是边AD、AB、BC、CD上的点，若AE=AF=CG=CH，问AE取何值时，四边形EFGH的面积最大？并求最大的面积．
的取值范围．
|=
.设
=a, 
=b, 
=c,求|a+b+c|.