题目内容
已知O是坐标原点,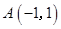 ,若点
,若点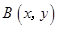 为平面区域
为平面区域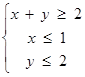 上一动点,则
上一动点,则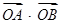 的取值范围是( )
的取值范围是( )
A.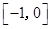 | B.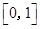 | C.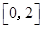 | D.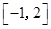 |
C
解析试题分析:根据题意可知,点B在区域为直角三角形,那么点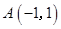 ,因此设
,因此设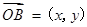 可知
可知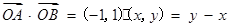 ,则目标函数为二元一次函数,那么借助于直线的截距的变换情况,平移直线z=y-x,然后当直线平移到点(1,1)点时最小为0,平移到点(0,2)时目标函数最大,且为2,故选C.
,则目标函数为二元一次函数,那么借助于直线的截距的变换情况,平移直线z=y-x,然后当直线平移到点(1,1)点时最小为0,平移到点(0,2)时目标函数最大,且为2,故选C.
考点:本试题考查了线性规划的简单运用。
点评:解决该试题的关键是能准确的表示不等式组的区域,同时能利用向量的数量积公式表示出目标函数,然后借助于直线的截距变化来分析得到最值,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 是
是 的重心,且
的重心,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
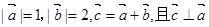 ,则向量
,则向量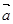 与
与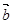 的夹角为( )
的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
点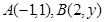 ,向量
,向量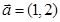 ,若
,若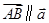 ,则实数
,则实数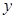 的值为
的值为
| A.5 | B.6 | C.7 | D.8 |
已知 ,O是坐标原点,则
,O是坐标原点,则 等于
等于
A. | B. | C. | D. |
如图,在四边形ABCD中,AB⊥BC,AD⊥DC,.若 则
则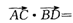 ( )
( )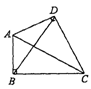
| A.a2-b2 | B.b2-a2 | C.a2+b2 | D.ab |
已知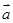 =(-3,2,5),b=(1,x,-1),且
=(-3,2,5),b=(1,x,-1),且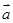 ⊥
⊥ ,则x的值为
,则x的值为
| A.3 | B.4 | C.5 | D.6 |
已知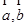 均为单位向量,它们的夹角为60°,那么,
均为单位向量,它们的夹角为60°,那么,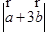 等于( )
等于( )
A. | B.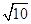 | C.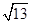 | D.4 |
已知向量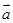 、
、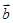 不共线,
不共线, ,如果
,如果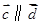 ,那么
,那么
A.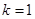 且 且 与 与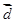 同向 同向 | B.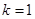 且 且 与 与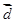 反向 反向 |
C.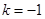 且 且 与 与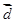 同向 同向 | D.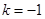 且 且 与 与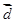 反向 反向 |