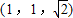题目内容
如图,建立空间直角坐标系D-xyz.正方体ABCD-A1B1C1D1的棱长为1,点P在面对角线A1B上,点Q在面对角线B1C上.
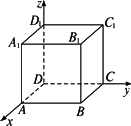
(1)当点P是对角线A1B的中点,点Q在对角线B1C上运动时,探究|PQ|的最小值;
(2)当点Q是对角线B1C的中点,点P在对角线A1B上运动时,探究|PQ|的最小值;
(3)当点P在对角线A1B上运动,点Q在对角线B1C上运动时,探究|PQ|的最小值.
答案:
解析:
提示:
解析:
|
解:如题图,由题意知:点A1(1,0,1)、点B1(1,1,1)、点B(1,1,0)、点C(0,1,0). (1)当点P是对角线A1B的中点,则由投影概念知点P(1, 点Q在对角线B1C上运动,设点Q(a,1,a),a∈[0,1]. 由空间两点间的距离公式 得|PQ|= 当a= (2)当点Q是对角线B1C的中点,则由投影概念知点Q( 得|PQ|= 当a= (3)当点P在对角线A1B上运动,点Q在对角线B1C上运动时,设点P(1,a,1-a)、点Q(b,1,b),a、b∈[0,1].由空间两点间距离公式得 |PQ|= 当b= 此时点P(1, 深化升华:本题通过消元利用二次函数配方法求最值. |
提示:
|
考查空间两点间距离公式的应用及函数思想在解析几何中的应用. |

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与| DB1 |
A、(1,
| ||||||
B、(1,1,
| ||||||
C、(
| ||||||
D、(
|
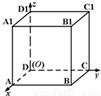 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与 共线的向量的坐标可以是( )
共线的向量的坐标可以是( )
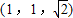
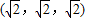
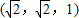
 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与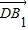 共线的向量的坐标可以是( )
共线的向量的坐标可以是( )



 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与 共线的向量的坐标可以是( )
共线的向量的坐标可以是( )
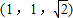


 以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与
以正方体ABCD-A1B1C1D1的顶点D为坐标原点O,如图,建立空间直角坐标系,则与 共线的向量的坐标可以是( )
共线的向量的坐标可以是( )