题目内容
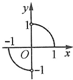 函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+x的解集为( )
函数y=f(x)的图象是圆心在原点的单位圆的两段弧(如图),则不等式f(x)<f(-x)+x的解集为( )A、{x|-
| ||||||||
B、{x|-1<x<-
| ||||||||
C、{x|-1<x<-
| ||||||||
D、{x|-
|
分析:本题考查的是函数的图象与图象变化问题.在解答时,应充分观察图形分析函数性质:奇偶性,将所求不等式化简,在集合自变量的不同范围分类讨论即可获得相应的不等式,进而获得问题的解答.
解答:解:由图象可知,该函数f(x)为奇函数,故原不等式可等价转化为f(x)<
x,
当x=1时,f(x)=0<
,显然成立,
当0<x<1时,f(x)=
,
∴1-x2<
x2,
∴
<x<1.
当-1≤x<0时,-
<
x,
∴1-x2>
x2,
∴-
<x<0.
综上所述,不等式f(x)<f(-x)+x的解集为
{x|-
<x<0或
<x≤1}.
故选:A.
| 1 |
| 2 |
当x=1时,f(x)=0<
| 1 |
| 2 |
当0<x<1时,f(x)=
| 1-x2 |
∴1-x2<
| 1 |
| 4 |
∴
2
| ||
| 5 |
当-1≤x<0时,-
| 1-x2 |
| 1 |
| 2 |
∴1-x2>
| 1 |
| 4 |
∴-
2
| ||
| 5 |
综上所述,不等式f(x)<f(-x)+x的解集为
{x|-
2
| ||
| 5 |
2
| ||
| 5 |
故选:A.
点评:本题考查的是函数的图象与图象变化问题.在解答过程当中充分体现了数形结合的思想、分类讨论的思想以及问题转化的思想.值得同学们体会反思.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示,给出关于f(x)的下列命题: