题目内容
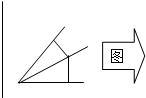 在平面几何中有如下特性:从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值.类比上述性质,请叙述在立体几何中相应地特性,并画出图形.不必证明.
在平面几何中有如下特性:从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值.类比上述性质,请叙述在立体几何中相应地特性,并画出图形.不必证明.分析:由平面图形的性质向空间物体的性质进行类比时,常用的思路有:由平面图形中点的性质类比推理出空间里的线的性质,由平面图形中线的性质类比推理出空间中面的性质,由平面图形中角的性质类比推理出空间中二面角的性质.我们可以根据已知中平面几何中,关于角的性质“从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值”,推断出一个空间几何中一个关于二面角的性质.
解答: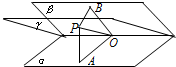 解:立体几何中相应地性质:
解:立体几何中相应地性质:
(1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的距离
之比为定值.
(2)从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的距离之比为定值.
(3)在空间,从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值.
(4)在空间,射线OD上任意一点P到射线OA、OB、OC的距离之比不变.
(5)在空间,射线OD上任意一点P到平面AOB、BOC、COA的距离之比不变.
(2)--(5)参考给分
 解:立体几何中相应地性质:
解:立体几何中相应地性质:(1)从二面角的棱出发的一个半平面内任意一点到二面角的两个面的距离
之比为定值.
(2)从二面角的棱上一点出发的一条射线上任意一点到二面角的两个面的距离之比为定值.
(3)在空间,从角的顶点出发的一条射线上任意一点到角两边的距离之比为定值.
(4)在空间,射线OD上任意一点P到射线OA、OB、OC的距离之比不变.
(5)在空间,射线OD上任意一点P到平面AOB、BOC、COA的距离之比不变.
(2)--(5)参考给分
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
相关题目
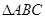 中,
中,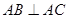 ,
点
,
点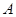 在
在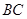 边上的射影为
边上的射影为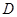 ,有
,有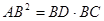 .”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥
.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的关系,可以得出的正确结论是:“在三棱锥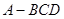 中,
中,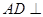 平面
平面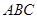 ,点
,点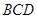 上的射影为
上的射影为 ,则有 .”
,则有 .”