题目内容
 已知椭圆的两焦点为F1(-
已知椭圆的两焦点为F1(-| 3 |
| 3 |
| ||
| 2 |
(Ⅰ)求此椭圆的方程.
(Ⅱ)设直线y=
| x |
| 2 |
(Ⅲ)若直线y=
| x |
| 2 |
分析:(I)求椭圆的方程即是求a,b两参数的值,由题设条件椭圆的两焦点为F1(-
,0),F2(
,0),离心率e=
.求出a,b即可得到椭圆的方程.
(II)本题中知道了直线l:y=
x+m,若l与此椭圆相交于P,Q两点,且|PQ|等于椭圆的短轴长,故可由弦长公式建立方程求出参数m的值.首先要将直线方程与椭圆方程联立,再利用弦长公式建立方程;
(III)设M(x1,y1),N(x2,y2),MN的中点为P(x,y),则x
+4y
=4,x
+4y
=4,利用设而不求的方法结合中点坐标公式即可求出线段MN的中点P的轨迹方程.
| 3 |
| 3 |
| ||
| 2 |
(II)本题中知道了直线l:y=
| 1 |
| 2 |
(III)设M(x1,y1),N(x2,y2),MN的中点为P(x,y),则x
2 1 |
2 1 |
2 2 |
2 2 |
解答:解:(I)设椭圆方程为
+
=1(a>b>0),则c=
,
=
,(4分)
∴a=2,b=1,所求椭圆方程
+y2=1.(5分)
(II)由
,消去y,得x2+2mx+2(m2-1)=0,…(6分)
则△=4m2-8(m2-1)>0得m2<2(*)
设P(x1,y1),Q(x2,y2),则x1+x2=-2m,x1x2=2m2-2,y1-y2=
(x1-x2)…(7分)
|PQ|=
=
=
=
•
=2…(9分)
解得,m=±
,满足(*)
∴m=±
.…(10分)
(III)设M(x1,y1),N(x2,y2),MN的中点为P(x,y),
则x
+4y
=4,x
+4y
=4,又x1+x2=2x,y1+y2=2y,
=
,
∴x+2y=0,因P在椭圆的内部,可求得-
<x<
,
∴线段MN的中点P的轨迹方程为x+2y=0,(-
<x<
).
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| c |
| a |
| ||
| 2 |
∴a=2,b=1,所求椭圆方程
| x2 |
| 4 |
(II)由
|
则△=4m2-8(m2-1)>0得m2<2(*)
设P(x1,y1),Q(x2,y2),则x1+x2=-2m,x1x2=2m2-2,y1-y2=
| 1 |
| 4 |
|PQ|=
| (x1-x2)2+(y1-y2)2 |
| ||
| 2 |
| (x1-x2)2-4x1x2 |
| ||
| 2 |
| 8-4m2 |
| 5 |
| 2-m2 |
解得,m=±
| ||
| 5 |
∴m=±
| ||
| 5 |
(III)设M(x1,y1),N(x2,y2),MN的中点为P(x,y),
则x
2 1 |
2 1 |
2 2 |
2 2 |
| y1-y2 |
| x1-x2 |
| 1 |
| 2 |
∴x+2y=0,因P在椭圆的内部,可求得-
| 2 |
| 2 |
∴线段MN的中点P的轨迹方程为x+2y=0,(-
| 2 |
| 2 |
点评:本题主要考查椭圆的标准方程和几何性质,直线方程,曲线和方程的关系等解析几何的基本思想方法和综合解题能力.解答的关键是利用方程思想利用设而不求的方法求出m值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
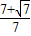


 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
). 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


