题目内容
设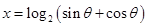 ,
,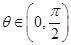 .
.
(1)求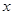 的取值范围;
的取值范围;
(2)设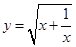 ,试问当
,试问当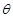 变化时,
变化时,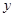 有没有最小值,如果有,求出这个最小值,如果没有,说明理由.
有没有最小值,如果有,求出这个最小值,如果没有,说明理由.
【答案】
(1)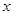 的取值范围是
的取值范围是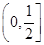 ;(2)当
;(2)当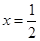 时,
时,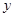 取最小值
取最小值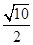 .
.
【解析】
试题分析:(1)先利用辅助角公式将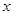 的表达式转化
的表达式转化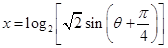 ,利用整体法计算
,利用整体法计算
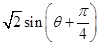 在
在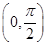 上的取值范围,再借助对数的运算确定
上的取值范围,再借助对数的运算确定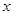 的取值范围;(2)设
的取值范围;(2)设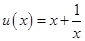 ,结合(1)中
,结合(1)中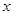 的取值范围,计算出
的取值范围,计算出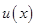 的取值范围,于是在根据不等式的性质求出
的取值范围,于是在根据不等式的性质求出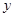 的最小值.
的最小值.
试题解析:(1)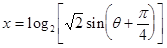 ,
,
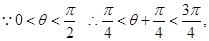
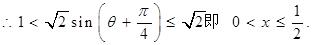
(2)设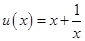 ,则
,则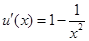 ,
,
当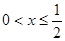 时,
时, ,
,
故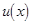 在
在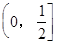 上是减函数,
上是减函数,
 当
当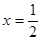 时,
时,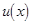 有最小值
有最小值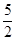 ,
,
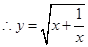 当
当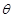 变化时,
变化时,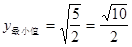 .
.
考点:1.辅助角公式;2.利用导数求最值

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
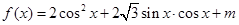 .其中
.其中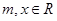
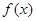 的最小正周期;
的最小正周期;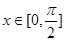 时,求实数
时,求实数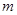 的值,使函数
的值,使函数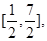 并求此时
并求此时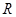 上的对称中心.
上的对称中心.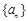 满足
满足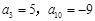 .
.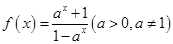 ,
,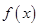 的反函数
的反函数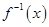 ;
;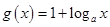 ,当
,当
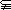
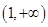 ,
,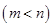 时,
时,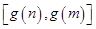 ,求
,求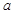 的取值范围.
的取值范围.