题目内容
将棱长相等的正方体按图所示方式固定摆放,其中第1堆只有一层,就一个正方体;第2,3,…,n堆分别有二层,三层,…,n层,每堆最顶层都只有一个正方体,以f(n)表示第n堆的正方体总数,则f(3)=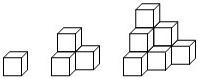
分析:观察图形,结合已知可得f(1)=1,f(2)=4,f(3)=10
由图中的规律可得f(n)-f(n-1)=(1+2+3+…+n)
从而可得f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]
代入可求
由图中的规律可得f(n)-f(n-1)=(1+2+3+…+n)
从而可得f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]
代入可求
解答:解:显然,f(1)=1,f(2)=4,f(3)=10
∵f(k)=f(k-1)+(1+2+3+…+k)=f(x-1)+
(k2+k),
∴f(k)-f(k-1)=(1+2+3+…+k)=
(k2+k),
从而f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]
=1+
(22+2)+
(32+3)+…+
(n2+n)
=
(12+22+32+…+n2)+
(1+2+3+…+n)
=
×
n(n+1)(2n+1)+
×
n(n+1)
=
n(n+1)(2n+1)
故答案为:10;
∵f(k)=f(k-1)+(1+2+3+…+k)=f(x-1)+
| 1 |
| 2 |
∴f(k)-f(k-1)=(1+2+3+…+k)=
| 1 |
| 2 |
从而f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 6 |
故答案为:10;
| n(n+1)(n+2) |
| 6 |
点评:本题主要考查了数列的通项公式在实际中的应用,解决本题的关键有两点:①由图形中的摆放归纳出一般规律f(k)-f(k-1)=(1+2+3+…+k)②要能利用跌代的方法求f(n).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 将棱长相等的正方体按如右图所示的形状摆放,从上往下依次为第1层,第2层,第3层….则第2005层正方体的个数是( )
将棱长相等的正方体按如右图所示的形状摆放,从上往下依次为第1层,第2层,第3层….则第2005层正方体的个数是( )| A、4011 | B、4009 | C、2011015 | D、2009010 |
 将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第一层、第二层、第三层…,则第2004层正方体的个数是( )
将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第一层、第二层、第三层…,则第2004层正方体的个数是( ) 将棱长相等的正方体按图所示的形状摆放,从上往下依次为第1层,第2层,第3层,…,则第6层正方体的个数是
将棱长相等的正方体按图所示的形状摆放,从上往下依次为第1层,第2层,第3层,…,则第6层正方体的个数是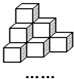 (2008•南汇区二模)将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第1层、第2层、第3层、….则第2008层正方体的个数是
(2008•南汇区二模)将棱长相等的正方体按如图所示的形状摆放,从上往下依次为第1层、第2层、第3层、….则第2008层正方体的个数是