题目内容
讨论下述函数的奇偶性:(1)f(x)=
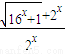 ,
,(2)f(x)=
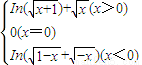 ,
,(3)f(x)=
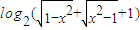 ,
,(4)f(x)=
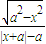 (常数a≠0).
(常数a≠0).
【答案】分析:(1)先化简函数,然后求出函数的定义域看其是否关于原点对称,最后判定f(-x)与f(x)的关系;
(2)分段函数的奇偶性的判定需要分段求解判定,分别在每一段上判定f(-x)与f(x)的关系;
(3)先求函数函数的定义域,然后化简函数解析式,可得函数f(x)的图象由两个点A(-1,0)与B(1,0)组成,
这两点既关于y轴对称,又关于原点对称,从而得到结论;
(4)要分a>0与a<0两类讨论,先求出函数的定义域,判定是否对称,然后根据f(-x)与f(x)的关系进一步判定奇偶性即可.
解答:解:(1)函数定义域为R,
先化简:f(x)=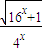 +1=
+1=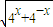 +1,
+1,
f(-x)=f(x),
∴f(x)为偶函数;
(2)须要分三段讨论:
①设x>0,∴-x>0
∴f(-x)=ln(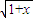 +
+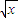 )=ln
)=ln =-ln(-
=-ln(-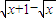 )=-f(x)
)=-f(x)
②设x<0,∴-x>0
∴f(-x)=ln(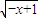 -
-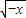 )=ln
)=ln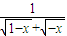 =-ln(
=-ln(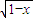 +
+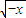 )=-f(x)
)=-f(x)
③当x=0时f(x)=0,也满足f(-x)=-f(x);
由①、②、③知,对x∈R有f(-x)=-f(x),
∴f(x)为奇函数;
(3)∵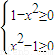 ⇒x2=1,
⇒x2=1,
∴函数的定义域为{x|x=±1},
∴f(x)=log21=0(x=±1),即f(x)的图象由两个点A(-1,0)与B(1,0)组成,
这两点既关于y轴对称,又关于原点对称,
∴f(x)既是奇函数,又是偶函数;
(4)∵x2≤a2,
∴要分a>0与a<0两类讨论,
①当a>0时,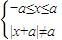 ⇒函数的定义域为(-a,0)∪(0,a)
⇒函数的定义域为(-a,0)∪(0,a)
∴|x+a|>0,∴f(x)=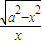 ,
,
∴当a>0时,f(x)为奇函数;
②当a<0时,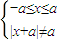 ⇒函数的定义域为(a,0)∪(0,-a)
⇒函数的定义域为(a,0)∪(0,-a)
∵|x+a|<0,∴f(x)=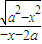 ,取定义域内关于原点对称的两点x1=
,取定义域内关于原点对称的两点x1=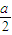 ,x2=-
,x2=-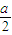 ,
,
∵f(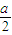 )±f(-
)±f(-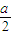 )=
)=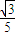 ±
±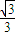 ≠0,
≠0,
∴当a<0时,f(x)既不是奇函数,也不是偶函数.
点评:本题主要考查了函数的奇偶性的判定,在定义域关于原点对称的前提下,可根据定义判定函数奇偶性.
(2)分段函数的奇偶性的判定需要分段求解判定,分别在每一段上判定f(-x)与f(x)的关系;
(3)先求函数函数的定义域,然后化简函数解析式,可得函数f(x)的图象由两个点A(-1,0)与B(1,0)组成,
这两点既关于y轴对称,又关于原点对称,从而得到结论;
(4)要分a>0与a<0两类讨论,先求出函数的定义域,判定是否对称,然后根据f(-x)与f(x)的关系进一步判定奇偶性即可.
解答:解:(1)函数定义域为R,
先化简:f(x)=
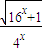 +1=
+1=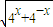 +1,
+1,f(-x)=f(x),
∴f(x)为偶函数;
(2)须要分三段讨论:
①设x>0,∴-x>0
∴f(-x)=ln(
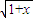 +
+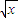 )=ln
)=ln =-ln(-
=-ln(-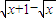 )=-f(x)
)=-f(x)②设x<0,∴-x>0
∴f(-x)=ln(
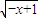 -
-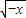 )=ln
)=ln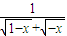 =-ln(
=-ln(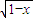 +
+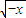 )=-f(x)
)=-f(x)③当x=0时f(x)=0,也满足f(-x)=-f(x);
由①、②、③知,对x∈R有f(-x)=-f(x),
∴f(x)为奇函数;
(3)∵
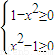 ⇒x2=1,
⇒x2=1,∴函数的定义域为{x|x=±1},
∴f(x)=log21=0(x=±1),即f(x)的图象由两个点A(-1,0)与B(1,0)组成,
这两点既关于y轴对称,又关于原点对称,
∴f(x)既是奇函数,又是偶函数;
(4)∵x2≤a2,
∴要分a>0与a<0两类讨论,
①当a>0时,
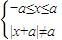 ⇒函数的定义域为(-a,0)∪(0,a)
⇒函数的定义域为(-a,0)∪(0,a)∴|x+a|>0,∴f(x)=
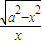 ,
,∴当a>0时,f(x)为奇函数;
②当a<0时,
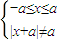 ⇒函数的定义域为(a,0)∪(0,-a)
⇒函数的定义域为(a,0)∪(0,-a)∵|x+a|<0,∴f(x)=
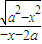 ,取定义域内关于原点对称的两点x1=
,取定义域内关于原点对称的两点x1=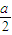 ,x2=-
,x2=-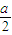 ,
,∵f(
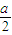 )±f(-
)±f(-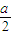 )=
)=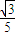 ±
±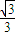 ≠0,
≠0,∴当a<0时,f(x)既不是奇函数,也不是偶函数.
点评:本题主要考查了函数的奇偶性的判定,在定义域关于原点对称的前提下,可根据定义判定函数奇偶性.

练习册系列答案
相关题目
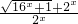 ,
,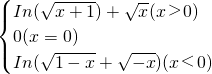 ,
,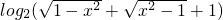 ,
,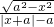 (常数a≠0).
(常数a≠0).