题目内容
16、下列5个判断:
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;
②函数y=2x-1与函数y=log2(x+1)的图象关于直线y=x对称;
③函数y=In(x2+1)的值域是R;
④函数y=2|x|的最小值是1;
⑤在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称.
其中正确的是
①若f(x)=x2-2ax在[1,+∞)上增函数,则a=1;
②函数y=2x-1与函数y=log2(x+1)的图象关于直线y=x对称;
③函数y=In(x2+1)的值域是R;
④函数y=2|x|的最小值是1;
⑤在同一坐标系中函数y=2x与y=2-x的图象关于y轴对称.
其中正确的是
②④⑤
.分析:①若f(x)[1,+∞)上增函数,只需对称轴在区间的左侧即可.
②求出y=2x-1的反函数若与y=log2(x+1)一致,则成立.
③由x2+1≥1,可求得其值域④作出函数y=2|x|的图象.
⑤在同一坐标系中作出函数y=2x与y=2-x的图象一目了然了.
②求出y=2x-1的反函数若与y=log2(x+1)一致,则成立.
③由x2+1≥1,可求得其值域④作出函数y=2|x|的图象.
⑤在同一坐标系中作出函数y=2x与y=2-x的图象一目了然了.
解答: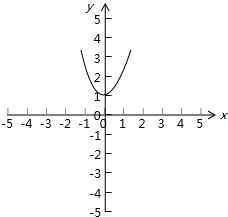 解:①若f(x)=x2-2ax在[1,+∞)上增函数,则a≤1;不正确.
解:①若f(x)=x2-2ax在[1,+∞)上增函数,则a≤1;不正确.
②解函数y=2x-1的反函数为y=log2(x+1),所以其图象关于直线y=x对称;正确.
③∵x2+1≥1,所以其值域是[0,+∞);不正确.
④作出函数y=2|x|的图象,如图所示,正确.
⑤在同一坐标系中函数y=2x与y=2-x的图象情境如④,可知关于y轴对称.正确.
故答案为:②④⑤
 解:①若f(x)=x2-2ax在[1,+∞)上增函数,则a≤1;不正确.
解:①若f(x)=x2-2ax在[1,+∞)上增函数,则a≤1;不正确.②解函数y=2x-1的反函数为y=log2(x+1),所以其图象关于直线y=x对称;正确.
③∵x2+1≥1,所以其值域是[0,+∞);不正确.
④作出函数y=2|x|的图象,如图所示,正确.
⑤在同一坐标系中函数y=2x与y=2-x的图象情境如④,可知关于y轴对称.正确.
故答案为:②④⑤
点评:本题主要考查函数的单调性,互为反函数图象间的关系,基本函数的图象的变换,突出了函数图象,考查了数形结合的解题能力.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
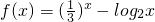 ,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为
,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为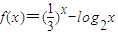 ,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为( )
,正实数a、b、c满足f(c)<0<f(a)<f(b).,若实数d是函数f(x)的一个零点,那么下列5个判断:①d<a;②d>b;③d<c;④c<a;⑤a<b.其中可能成立的个数为( )