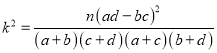题目内容
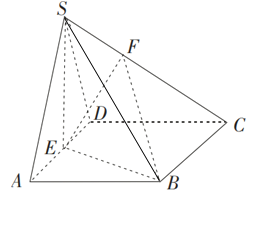
【题目】已知四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠BAD=60°,SA=SD=2![]() ,点E是棱AD的中点,点F在棱SC上,且
,点E是棱AD的中点,点F在棱SC上,且![]() λ,SA//平面BEF.
λ,SA//平面BEF.
(1)求实数λ的值;
(2)求三棱锥F﹣EBC的体积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)连接AC,设AC∩BE=G,根据线面平行的性质定理,结合平行线的性质,通过相似三角形的性质进行求解即可;
(2)根据菱形的性质、勾股定理的逆定理、线面垂直的判定定理,结合三棱锥的体积公式,三角形的面积公式进行求解即可.
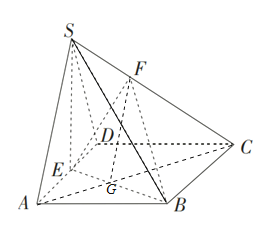
(1)连接AC,设AC∩BE=G,则平面SAC∩平面EFB=FG,
∵SA∥平面EFB,∴SA∥FG,
∵△GEA∽△GBC,∴![]() ,
,
∴![]() ,
,
得SF![]() ,即
,即![]() ;
;
(2)∵SA=SD=2![]() ,∴SE⊥AD,SE=4.
,∴SE⊥AD,SE=4.
又∵AB=AD=4,∠BAD=60°,∴BE=2![]() .
.
∴SE2+BE2=SB2,则SE⊥BE.![]() ,
,![]() 平面ABCD,
平面ABCD,
∴SE⊥平面ABCD,
∴![]() .
.

练习册系列答案
相关题目
【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答,统计情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男 同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择几何题的8名女生中任意抽取两人对他们的答题进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |