题目内容
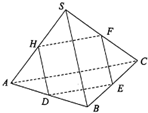 在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB、BC、SC、SA交于D、E、F、H分别是AB、BC、SA、SC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为( )
在三棱锥S-ABC中,△ABC是边长为6的正三角形,SA=SB=SC=15,平面DEFH分别与AB、BC、SC、SA交于D、E、F、H分别是AB、BC、SA、SC的中点,如果直线SB∥平面DEFH,那么四边形DEFH的面积为( )A、
| ||||
B、
| ||||
| C、45 | ||||
D、45
|
分析:根据条件只要证明四边形DEFH是矩形即可得到结论.
解答: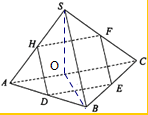 解:∵D、E、F、H分别是AB、BC、SA、SC的中点,
解:∵D、E、F、H分别是AB、BC、SA、SC的中点,
∴DE∥AC,FH∥AC,DH∥SB.EF∥SB,
则四边形DEFH是平行四边形,且HD=
SB=
,DE=
AC=3
取AC的中点O,连结OB,
∵SA=SC=15,AB=BC=6,
∴AC⊥SO,AC⊥OB,
∵S0∩OB=O,
∴AO⊥平面SOB,
∴AO⊥SB,
则HD⊥DE,
即四边形DEFH是矩形,
∴四边形DEFH的面积S=
×3=
,
故选:A.
 解:∵D、E、F、H分别是AB、BC、SA、SC的中点,
解:∵D、E、F、H分别是AB、BC、SA、SC的中点,∴DE∥AC,FH∥AC,DH∥SB.EF∥SB,
则四边形DEFH是平行四边形,且HD=
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
取AC的中点O,连结OB,
∵SA=SC=15,AB=BC=6,
∴AC⊥SO,AC⊥OB,
∵S0∩OB=O,
∴AO⊥平面SOB,
∴AO⊥SB,
则HD⊥DE,
即四边形DEFH是矩形,
∴四边形DEFH的面积S=
| 15 |
| 2 |
| 45 |
| 2 |
故选:A.
点评:本题主要考查线面平行的判断和应用,根据条件先判断四边形DEFH是平行四边形,然后根据线面垂直的判定定理证明四边形DEFH是矩形是解决本题的关键.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为1的等边三角形,∠BAC=90°,O为BC中点.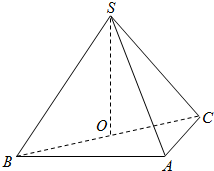 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点. 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C. 如图,在三棱锥S-ABC中,
如图,在三棱锥S-ABC中,