题目内容
(1)设a1,a2,…,an是各项均不为零的n(n≥4)项等差数列,且公差d≠0,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列.(i)当n=4时,求
 的数值;
的数值;(ii)求n的所有可能值.
(2)求证:对于给定的正整数n(n≥4),存在一个各项及公差均不为零的等差数列b1,b2,…,bn,其中任意三项(按原来的顺序)都不能组成等比数列.
【答案】分析:(1)根据题意,对n=4,n=5时数列中各项的情况逐一讨论,利用反证法结合等差数列的性质进行论证,进而推广到n≥4的所有情况.
(2)利用反证法结合等差数列的性质进行论证即可.
解答:解:(1)①当n=4时,a1,a2,a3,a4中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0.
若删去a2,则a32=a1•a4,即(a1+2d)2=a1•(a1+3d)化简得a1+4d=0,得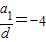
若删去a3,则a22=a1•a4,即(a1+d)2=a1•(a1+3d)化简得a1-d=0,得
综上,得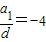 或
或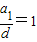 .
.
②当n=5时,a1,a2,a3,a4,a5中同样不可能删去a1,a2,a4,a5,否则出现连续三项.
若删去a3,则a1•a5=a2•a4,即a1(a1+4d)=(a1+d)•(a1+3d)化简得3d2=0,因为d≠0,所以a3不能删去;
当n≥6时,不存在这样的等差数列.事实上,在数列a1,a2,a3,…,an-2,an-1,an中,由于不能删去首项或末项,
若删去a2,则必有a1•an=a3•an-2,这与d≠0矛盾;
同样若删去an-1也有a1•an=a3•an-2,这与d≠0矛盾;
若删去a3,,an-2中任意一个,则必有a1•an=a2•an-1,这与d≠0矛盾.(或者说:当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)
综上所述,n=4.
(2)假设对于某个正整数n,存在一个公差为d的n项等差数列b1,b2,bn,其中bx+1,by+1,bz+1(0≤x<y<z≤n-1)为任意三项成等比数列,则b2y+1=bx+1•bz+1,即(b1+yd)2=(b1+xd)•(b1+zd),化简得(y2-xz)d2=(x+z-2y)b1d(*)
由b1d≠0知,y2-xz与x+z-2y同时为0或同时不为0
当y2-xz与x+z-2y同时为0时,有x=y=z与题设矛盾.
故y2-xz与x+z-2y同时不为0,所以由(*)得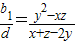
因为0≤x<y<z≤n-1,且x、y、z为整数,所以上式右边为有理数,从而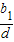 为有理数.
为有理数.
于是,对于任意的正整数n(n≥4),只要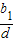 为无理数,相应的数列就是满足题意要求的数列.
为无理数,相应的数列就是满足题意要求的数列.
例如n项数列1,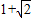 ,
,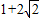 ,,
,,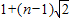 满足要求.
满足要求.
点评:本题是一道探究性题目,考查了等差数列和等比数列的通项公式,以及学生的运算能力和推理论证能力.
(2)利用反证法结合等差数列的性质进行论证即可.
解答:解:(1)①当n=4时,a1,a2,a3,a4中不可能删去首项或末项,否则等差数列中连续三项成等比数列,则推出d=0.
若删去a2,则a32=a1•a4,即(a1+2d)2=a1•(a1+3d)化简得a1+4d=0,得
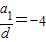
若删去a3,则a22=a1•a4,即(a1+d)2=a1•(a1+3d)化简得a1-d=0,得

综上,得
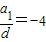 或
或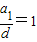 .
.②当n=5时,a1,a2,a3,a4,a5中同样不可能删去a1,a2,a4,a5,否则出现连续三项.
若删去a3,则a1•a5=a2•a4,即a1(a1+4d)=(a1+d)•(a1+3d)化简得3d2=0,因为d≠0,所以a3不能删去;
当n≥6时,不存在这样的等差数列.事实上,在数列a1,a2,a3,…,an-2,an-1,an中,由于不能删去首项或末项,
若删去a2,则必有a1•an=a3•an-2,这与d≠0矛盾;
同样若删去an-1也有a1•an=a3•an-2,这与d≠0矛盾;
若删去a3,,an-2中任意一个,则必有a1•an=a2•an-1,这与d≠0矛盾.(或者说:当n≥6时,无论删去哪一项,剩余的项中必有连续的三项)
综上所述,n=4.
(2)假设对于某个正整数n,存在一个公差为d的n项等差数列b1,b2,bn,其中bx+1,by+1,bz+1(0≤x<y<z≤n-1)为任意三项成等比数列,则b2y+1=bx+1•bz+1,即(b1+yd)2=(b1+xd)•(b1+zd),化简得(y2-xz)d2=(x+z-2y)b1d(*)
由b1d≠0知,y2-xz与x+z-2y同时为0或同时不为0
当y2-xz与x+z-2y同时为0时,有x=y=z与题设矛盾.
故y2-xz与x+z-2y同时不为0,所以由(*)得
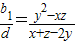
因为0≤x<y<z≤n-1,且x、y、z为整数,所以上式右边为有理数,从而
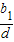 为有理数.
为有理数.于是,对于任意的正整数n(n≥4),只要
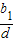 为无理数,相应的数列就是满足题意要求的数列.
为无理数,相应的数列就是满足题意要求的数列.例如n项数列1,
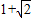 ,
,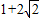 ,,
,,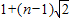 满足要求.
满足要求.点评:本题是一道探究性题目,考查了等差数列和等比数列的通项公式,以及学生的运算能力和推理论证能力.

练习册系列答案
相关题目
 的数值;
的数值; 的数值;
的数值;