题目内容
(1)设a1,a2,…,an是各项均不为零的n(n≥4)项等差数列,且公差d≠0,若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列(i)当n=4时,求
 的数值;
的数值;(ii)求n的所有可能值.
(2)求证:存在一个各项及公差均不为零的n(n≥4)项等差数列,任意删去其中的k项(1≤k≤n-3),都不能使剩下的项(按原来的顺序)构成等比数列.
【答案】分析:(1)(i)当n=4时,数列的公差d≠0,删去的项只可能为a2或a3.分别讨论推出数列的情况,然后求解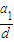 的值.
的值.
(ii)当n≥6时,从数列中删去任意一项后得到的数列,必有原数列中的连续三项,从而这三项既成等差数列又成等比数列,数列的公差必为0,这与题设矛盾.推出数列的项数n≤5.然后讨论当n=4,n=5时,满足题设的数列项数即可.
(2)首先找出一个等差数列b1,b2,…,bn(n≥4)的首项b1与公差d'的比值为无理数,则此等差数列满足题设要求.假设删去等差数列b1,b2,…,bn(n≥4)中的k(1≤k≤n-3)项后,新数列构成等比数列,说明新数列中的连续三项为不满足题意,然后推出首项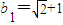 ,公差d′=1.相应的等差数列
,公差d′=1.相应的等差数列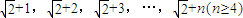 是一个满足题设要求的数列.
是一个满足题设要求的数列.
解答:解:首先证明一个“基本事实”
一个等差数列中,若有连续三项成等比数列,则这个数列的公差d=0.
事实上,设这个数列中的连续三项a-d,a,a+d成等比数列,则a2=(a-d)(a+d),由此得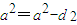 ,故d=0.
,故d=0.
(1)(i)当n=4时,由于数列的公差d≠0,故由“基本事实“推知,删去的项只可能为a2或a3.
①若删去a2,则由a1,a3,a4成等比数列,得 .
.
因d≠0,故由上式得a1=-4d,即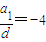 .此时数列为-4d,-3d,-2d,-d,满足题设.
.此时数列为-4d,-3d,-2d,-d,满足题设.
②若删去a3,则a1,a2,a4由成等比数列,得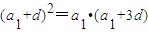 .
.
因d≠0,故由上式得a1=d,即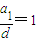 .此时数列为d,2d,3d,4d满足题设.
.此时数列为d,2d,3d,4d满足题设.
综上可知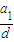 的值为-4或1.
的值为-4或1.
(ii)当n≥6时,则从满足题设的数列a1,a2,a3,…,an中删去任意一项后得到的数列,必有原数列中的连续三项,从而这三项既成等差数列又成等比数列,故由“基本事实”知,数列a1,a2,a3,…,an的公差必为0,这与题设矛盾.所以满足题设的数列的项数n≤5.
又因题设n≥4,故n=4或n=5.
当n=4时,由(i)中的讨论知存在满足题设的数列.
当n=5时,若存在满足题设的数列a1,a2,a3,a4,a5则由“基本事实”知,删去的项只能是a3,从a1,a2,a4,a5而成等比数列,故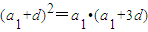 ,
,
及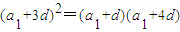 .分别化简上述两个等式,得
.分别化简上述两个等式,得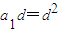 及
及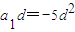 ,
,
故d=0.矛盾.因此,不存在满足题设的项数为5的等差数列. 综上可知,n只能为4.
(2)我们证明:若一个等差数列b1,b2,…,bn(n≥4)的首项b1与公差d'的比值为无理数,
则此等差数列满足题设要求.
证明如下:
假设删去等差数列b1,b2,…,bn(n≥4)中的k(1≤k≤n-3)项后,
得到的新数列(按原来的顺序)构成等比数列,
设此新数列中的连续三项为b1+m1d',b1+m2d',b1+m3d'(0≤m1<m2<m3≤n-1),于是有 ,化简得
,化简得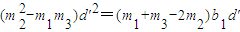 …(*)
…(*)
由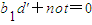 知,
知,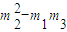 与m1+m3-2m2同时为零或同时不为零.
与m1+m3-2m2同时为零或同时不为零.
若m1+m3-2m2=0,且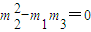 ,则有
,则有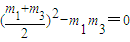 ,
,
即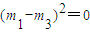 ,得m1=m3,从而m1=m2=m3,矛盾.
,得m1=m3,从而m1=m2=m3,矛盾.
因此,m1+m3-2m2与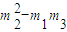 都不为零,故由(*)式得
都不为零,故由(*)式得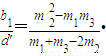 …(**)
…(**)
因为m1,m2,m3均为非负整数,所以(**)式右边是有理数,
而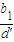 是一个无理数,所以(**)式不成立.这就证明了上述结果.
是一个无理数,所以(**)式不成立.这就证明了上述结果.
因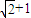 是一个无理数.因此,取首项
是一个无理数.因此,取首项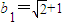 ,公差d′=1.
,公差d′=1.
则相应的等差数列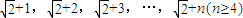 是一个满足题设要求的数列.
是一个满足题设要求的数列.
点评:本题以等差数列、等比数列为平台,主要考查学生的探索与推理能力.利用基本事实,反证法的应用,找出满足题意的一个数列是解题的难点也是关键点,本题属难题.
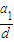 的值.
的值.(ii)当n≥6时,从数列中删去任意一项后得到的数列,必有原数列中的连续三项,从而这三项既成等差数列又成等比数列,数列的公差必为0,这与题设矛盾.推出数列的项数n≤5.然后讨论当n=4,n=5时,满足题设的数列项数即可.
(2)首先找出一个等差数列b1,b2,…,bn(n≥4)的首项b1与公差d'的比值为无理数,则此等差数列满足题设要求.假设删去等差数列b1,b2,…,bn(n≥4)中的k(1≤k≤n-3)项后,新数列构成等比数列,说明新数列中的连续三项为不满足题意,然后推出首项
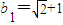 ,公差d′=1.相应的等差数列
,公差d′=1.相应的等差数列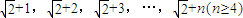 是一个满足题设要求的数列.
是一个满足题设要求的数列.解答:解:首先证明一个“基本事实”
一个等差数列中,若有连续三项成等比数列,则这个数列的公差d=0.
事实上,设这个数列中的连续三项a-d,a,a+d成等比数列,则a2=(a-d)(a+d),由此得
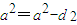 ,故d=0.
,故d=0.(1)(i)当n=4时,由于数列的公差d≠0,故由“基本事实“推知,删去的项只可能为a2或a3.
①若删去a2,则由a1,a3,a4成等比数列,得
 .
.因d≠0,故由上式得a1=-4d,即
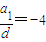 .此时数列为-4d,-3d,-2d,-d,满足题设.
.此时数列为-4d,-3d,-2d,-d,满足题设.②若删去a3,则a1,a2,a4由成等比数列,得
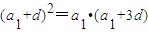 .
.因d≠0,故由上式得a1=d,即
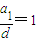 .此时数列为d,2d,3d,4d满足题设.
.此时数列为d,2d,3d,4d满足题设.综上可知
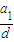 的值为-4或1.
的值为-4或1.(ii)当n≥6时,则从满足题设的数列a1,a2,a3,…,an中删去任意一项后得到的数列,必有原数列中的连续三项,从而这三项既成等差数列又成等比数列,故由“基本事实”知,数列a1,a2,a3,…,an的公差必为0,这与题设矛盾.所以满足题设的数列的项数n≤5.
又因题设n≥4,故n=4或n=5.
当n=4时,由(i)中的讨论知存在满足题设的数列.
当n=5时,若存在满足题设的数列a1,a2,a3,a4,a5则由“基本事实”知,删去的项只能是a3,从a1,a2,a4,a5而成等比数列,故
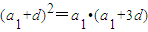 ,
,及
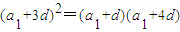 .分别化简上述两个等式,得
.分别化简上述两个等式,得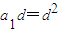 及
及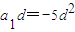 ,
,故d=0.矛盾.因此,不存在满足题设的项数为5的等差数列. 综上可知,n只能为4.
(2)我们证明:若一个等差数列b1,b2,…,bn(n≥4)的首项b1与公差d'的比值为无理数,
则此等差数列满足题设要求.
证明如下:
假设删去等差数列b1,b2,…,bn(n≥4)中的k(1≤k≤n-3)项后,
得到的新数列(按原来的顺序)构成等比数列,
设此新数列中的连续三项为b1+m1d',b1+m2d',b1+m3d'(0≤m1<m2<m3≤n-1),于是有
 ,化简得
,化简得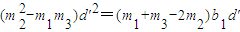 …(*)
…(*)由
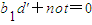 知,
知,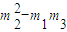 与m1+m3-2m2同时为零或同时不为零.
与m1+m3-2m2同时为零或同时不为零.若m1+m3-2m2=0,且
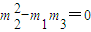 ,则有
,则有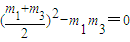 ,
,即
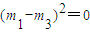 ,得m1=m3,从而m1=m2=m3,矛盾.
,得m1=m3,从而m1=m2=m3,矛盾.因此,m1+m3-2m2与
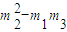 都不为零,故由(*)式得
都不为零,故由(*)式得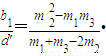 …(**)
…(**)因为m1,m2,m3均为非负整数,所以(**)式右边是有理数,
而
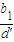 是一个无理数,所以(**)式不成立.这就证明了上述结果.
是一个无理数,所以(**)式不成立.这就证明了上述结果.因
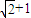 是一个无理数.因此,取首项
是一个无理数.因此,取首项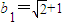 ,公差d′=1.
,公差d′=1.则相应的等差数列
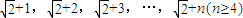 是一个满足题设要求的数列.
是一个满足题设要求的数列.点评:本题以等差数列、等比数列为平台,主要考查学生的探索与推理能力.利用基本事实,反证法的应用,找出满足题意的一个数列是解题的难点也是关键点,本题属难题.

练习册系列答案
相关题目
 的数值;
的数值;