题目内容
下列说法中正确的个数是( )
(1)满足
-
=4的点P(x,y)的轨迹是双曲线
(2)到直线3x+y-2=0的距离等于到点P(1,-1)的距离的点的轨迹为抛物线
(3)1,100的等比中项为10
(4)向量内积运算满足结合律.
(1)满足
| x2+(y-2)2 |
| x2+(y+2)2 |
(2)到直线3x+y-2=0的距离等于到点P(1,-1)的距离的点的轨迹为抛物线
(3)1,100的等比中项为10
(4)向量内积运算满足结合律.
分析:(1)
-
=4表示一条射线;
(2)到直线3x+y-2=0的距离等于到点P(1,-1)的距离的点的轨迹一条直线;
(3)1,100的等比中项为±10;
(4)向量内积运算不满足结合律.
| x2+(y-2)2 |
| x2+(y+2)2 |
(2)到直线3x+y-2=0的距离等于到点P(1,-1)的距离的点的轨迹一条直线;
(3)1,100的等比中项为±10;
(4)向量内积运算不满足结合律.
解答:解:(1)
-
=4表示到(0,2)和(0,-2)的距离之差为4的点的集合,
它所表示的是一条射线,故(1)不正确;
(2)∵点P(1,-1)在直线3x+y-2=0上,
∴到直线3x+y-2=0的距离等于到点P(1,-1)的距离的点的轨迹为过点P且垂直于直线3x+y-2=0的一条直线,
故(2)不正确;
(3)1,100的等比中项为±
=±10,故(3)不正确;
(4)向量内积运算不满足结合律,故(4)不正确.
故选A.
| x2+(y-2)2 |
| x2+(y+2)2 |
它所表示的是一条射线,故(1)不正确;
(2)∵点P(1,-1)在直线3x+y-2=0上,
∴到直线3x+y-2=0的距离等于到点P(1,-1)的距离的点的轨迹为过点P且垂直于直线3x+y-2=0的一条直线,
故(2)不正确;
(3)1,100的等比中项为±
| 1×100 |
(4)向量内积运算不满足结合律,故(4)不正确.
故选A.
点评:本题考查命题的真假判断及其应用,是基础题.解题时要注意双曲线、抛物线、等比中项、向量的数量积等基本知识点的合理运用.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
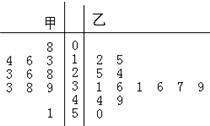 甲、已乙两名篮球运动员每场比赛的得分情况用茎叶图表示如下:
甲、已乙两名篮球运动员每场比赛的得分情况用茎叶图表示如下: