题目内容
已知函数 .
.
(Ⅰ)求 的极值;
的极值;
(II)判断y=f(x)的图像是否是中心对称图形,若是求出对称中心并证明,否则说明理由;
(III)设 的定义域为
的定义域为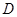 ,是否存在
,是否存在 .当
.当 时,
时, 的取值范围是
的取值范围是 ?若存在,求实数
?若存在,求实数 、
、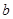 的值;若不存在,说明理由
的值;若不存在,说明理由
【答案】
(II)
点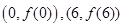 的中点是
的中点是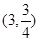 ,所以
,所以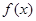 的图象的对称中心只可能是
的图象的对称中心只可能是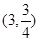 .
.
即点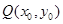 也在函数y=f(x)的图像上。
也在函数y=f(x)的图像上。
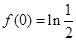 是
是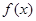 的一个极大值,
的一个极大值,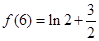 是
是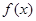 的一个极小值.
的一个极小值. 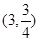
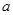 、
、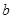 不存在
不存在
【解析】
解:(I) 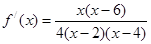 .注意到
.注意到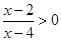 ,即
,即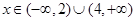 ,
,
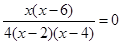 得
得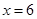 或
或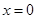 .所以当
.所以当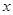 变化时,
变化时, 的变化情况如下表:
的变化情况如下表:
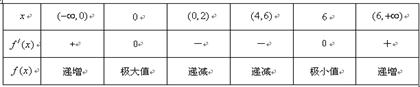
所以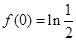 是
是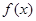 的一个极大值,
的一个极大值,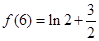 是
是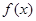 的一个极小值.
的一个极小值.
|
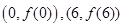 的中点是
的中点是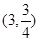 ,所以
,所以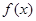 的图象的对称中心只可能是
的图象的对称中心只可能是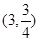 .
.
设 为
为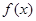 的图象上一点,
的图象上一点,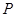 关于
关于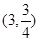 的对称点是Q
的对称点是Q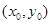 ,
,
因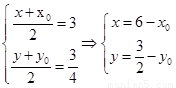 ,又
,又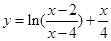
所以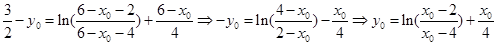 ,
,
|
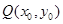 也在函数y=f(x)的图像上。
也在函数y=f(x)的图像上。
设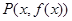 为
为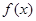 的图象上一点,
的图象上一点,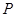 关于
关于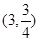 的对称点是
的对称点是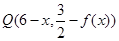 ……
……
(III) 假设存在实数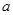 、
、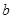 .
.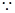
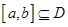 ,
,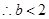 或
或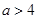 .
.
若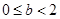 , 当
, 当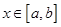 时,
时, 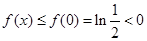 ,而
,而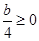
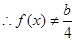 .故不可能…
.故不可能…
若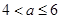 ,当
,当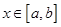 时,
时, 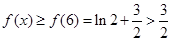 ,而
,而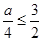
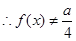 .故不可能….
.故不可能….
若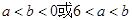 ,由
,由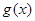 的单调递增区间是
的单调递增区间是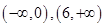 ,知
,知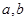 是
是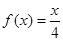 的两个解.而
的两个解.而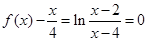 无解. 故此时
无解. 故此时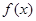 的取值范围是不可能是
的取值范围是不可能是 .
.
综上所述,假设错误,满足条件的实数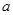 、
、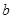 不存在.
不存在.

练习册系列答案
相关题目

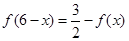

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.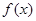 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求