题目内容
4.不等式x2-2x<0的解集是( )| A. | {x|0<x<2} | B. | {x|-2<x<0} | C. | {x|x<0,或x>2} | D. | {x|x<-2,或x>0} |
分析 先求相应二次方程x2-2x=0的两根,根据二次函数y=x2-2x的图象即可写出不等式的解集.
解答 解:方程x2-2x=0的两根为0,2,
且函数y=x2-2x的图象开口向上,
所以不等式x2-2x<0的解集为(0,2).
故选:A.
点评 本题考查一元二次不等式的解法,属基础题,深刻理解“三个二次”间的关系是解决该类题目的关键,解二次不等式的基本步骤是:求二次方程的根;作出草图;据图象写出解集.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知集合M={x|-1<x<3},N={-1,0,1,2,3},则M∩N=( )
| A. | {0,1,2} | B. | {-1,0,1,2} | C. | {-1,0,1,2,3} | D. | {-1,3} |
14.下列区间中,能使函数y=sinx与函数y=cosx同时单调递减的是( )
| A. | [0,$\frac{π}{3}$] | B. | [$\frac{2π}{3}$,$\frac{3π}{4}$] | C. | [$\frac{7π}{6}$,$\frac{3π}{2}$] | D. | [$\frac{5π}{3}$,2π] |
 , 集合
, 集合 ,
, 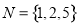 , 则集合
, 则集合 可以表示为
可以表示为  B.
B.
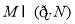 D.
D.
 中,
中, ,
, ,则数列
,则数列 项和
项和 等于( )
等于( )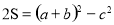 ,则tanC等于( )
,则tanC等于( ) B.
B.  C.
C. 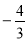 D.
D. 
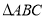 中,
中, ,则
,则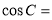 ( )
( )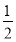 B.
B.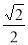 C.
C. D.
D.