题目内容
设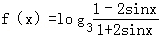 .
.
(1)判断函数y=f(x)的奇偶性;
(2)求函数y=f(x)的定义域和值域.
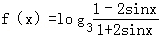 .
.(1)判断函数y=f(x)的奇偶性;
(2)求函数y=f(x)的定义域和值域.
(1)奇函数(2)定义域 ,k∈Z},值域为R
,k∈Z},值域为R
 ,k∈Z},值域为R
,k∈Z},值域为R试题分析:解:(1)∵
 0⇒﹣
0⇒﹣ <sinx<
<sinx< ⇒kπ﹣
⇒kπ﹣ <x<kπ+
<x<kπ+ ,k∈Z,定义域关于原点对称.
,k∈Z,定义域关于原点对称.∴f(﹣x)=log2
 =log2
=log2 =﹣log2
=﹣log2 =﹣f(x).
=﹣f(x).∴故其为奇函数;
(2)由上得:定义域
 ,k∈Z},
,k∈Z},∵
 =
= =﹣1+
=﹣1+ .
.而﹣
 <sinx<
<sinx< ⇒0<1+2sinx<2⇒
⇒0<1+2sinx<2⇒ >1⇒﹣1+
>1⇒﹣1+ >0⇒y=log3
>0⇒y=log3 的值域为R. ∴值域为R.
的值域为R. ∴值域为R.点评:解决的关键是对于复合函数单调性,以及三角函数的性质的熟练运用,属于基础题。

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 是
是 的内角,当
的内角,当 ,则
,则


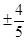

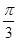 -
-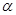 )=
)=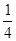 ,则cos(
,则cos(
 ( )其中
( )其中
 -cos
-cos
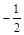


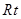 △ABC内有一内接正方形,它的一条边在斜边BC上,设AB=
△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=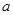 ,∠ABC
,∠ABC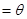
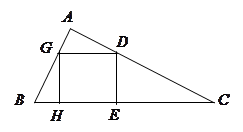
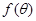 与正方形面积
与正方形面积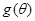 ;
;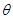 变化时,求
变化时,求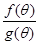 的最小值,并求出对应
的最小值,并求出对应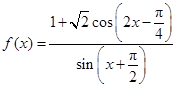 .
.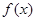 的定义域;
的定义域;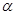 在第一象限且
在第一象限且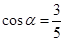 ,求
,求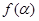 .
.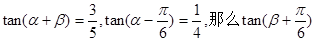 =( )
=( )



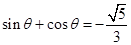 ,则
,则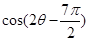 的值为( )
的值为( )


