题目内容
 数列{an}的前W项和为Sn,且Sn=
数列{an}的前W项和为Sn,且Sn=| n2+3n |
| 2 |
|
(I)求数列{an}的通项公式,并求数列{cn}的前n项和{Tn};
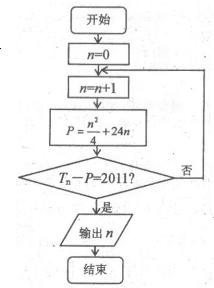
(II)张三同学利用第(I)问中的Tn设计了一个程序框图(如图),但李四同学认为这个程序如果被执行将会是一个“死循环”(即程序会永远循环下去,而无法结束).你是否同意李四同学的观点?请说明理由.
分析:(I)、根据题中数列{an}的前n项和为Sn,的公式便可推导出数列{an}的通项公式,根据给出的cn的通项公式,分别讨论当n为奇数和偶数时数列{cn}的前n项和{Tn};
(II)分别讨论当n为偶数和奇数时Tn-P的最终结果为2011,故李四的说法正确,该程序会是一个死循环.
(II)分别讨论当n为偶数和奇数时Tn-P的最终结果为2011,故李四的说法正确,该程序会是一个死循环.
解答:解:(I)当n=1时,a1=S1=
=2,
当n≥2时,an=Sn-Sn-1=
(n2+3n-(n-1)2-3(n-1)=n+1,
∴an=n+1(n),当n为偶数时,Tn=(a1+a3+…+an)+(22+24+…+2n)=
+
(2n-1),
当n为偶数时,Tn=(a1+a3+…+an)+(22+24+…+2n-1)=
+
(2n-1-1),
∴Tn=
;
(II)记Dn=Tn-P,则当n为偶数时,Dn=
+
(2n-1)-
-24n=
(2n-1)-
,
∴Dn+2-Dn=
(2n+1-1)-
-
(2n-1)-
=2n+2-47,
∴从第四项开始,数列{Dn}的偶数项开始递增,
而D2,D4,…,D10均小于2010,D12>2010,即n偶数时,Dn=2011,
当n为奇数时,Dn=
+
(2n-1-1)-
-24n=
(2n-1-1)-23n+
,
同理Dn+2-Dn=2n+1-46,
∴从第五项开始,数列{Dn}的奇数项开始递增,
而D1,D3,…,D11均小于2010,D13>2010,即n偶数时,Dn=2011,
故李四的说法正确.
| 1+3 |
| 2 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2 |
∴an=n+1(n),当n为偶数时,Tn=(a1+a3+…+an)+(22+24+…+2n)=
| n2+2n |
| 4 |
| 4 |
| 3 |
当n为偶数时,Tn=(a1+a3+…+an)+(22+24+…+2n-1)=
| n2+4n+3 |
| 4 |
| 4 |
| 3 |
∴Tn=
|
(II)记Dn=Tn-P,则当n为偶数时,Dn=
| n2+2n |
| 4 |
| 4 |
| 3 |
| n2 |
| 4 |
| 4 |
| 3 |
| 47n |
| 2 |
∴Dn+2-Dn=
| 4 |
| 3 |
| 47(n+2) |
| 2 |
| 4 |
| 3 |
| 47n |
| 2 |
∴从第四项开始,数列{Dn}的偶数项开始递增,
而D2,D4,…,D10均小于2010,D12>2010,即n偶数时,Dn=2011,
当n为奇数时,Dn=
| n2+4n+3 |
| 4 |
| 4 |
| 3 |
| n2 |
| 4 |
| 4 |
| 3 |
| 3 |
| 4 |
同理Dn+2-Dn=2n+1-46,
∴从第五项开始,数列{Dn}的奇数项开始递增,
而D1,D3,…,D11均小于2010,D13>2010,即n偶数时,Dn=2011,
故李四的说法正确.
点评:本题考查了数列的基本知识和前n项和的求法以及循环结构,考查了学生的计算能力和对数列、循环结构的综合掌握,解题时注意分类讨论思想和转化思想的运用,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 ,求数列{bn}的前n项和Sn w.w.w.k.s.5.u.c.o.m
,求数列{bn}的前n项和Sn w.w.w.k.s.5.u.c.o.m 

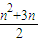 {an}数列{cn},满足cn=
{an}数列{cn},满足cn= ,
,