题目内容
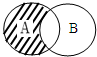 设A、B为非空集合,定义运算A*B为如图阴影部分表示的集合,若A={x|y=
设A、B为非空集合,定义运算A*B为如图阴影部分表示的集合,若A={x|y=| 2x-x2 |
分析:由题意可知,A={x|0≤x≤2},B={y|y>1},于是A∩B=(1,2],从而可得A∩[CuA∩B].
解答:解:由2x-x2≥0得0≤x≤2,
∴A={x|0≤x≤2},
同理可求B={y|y>1},
∴A∩B=(1,2],
∴A∩[CuA∩B]=[0,1].
故选A.
∴A={x|0≤x≤2},
同理可求B={y|y>1},
∴A∩B=(1,2],
∴A∩[CuA∩B]=[0,1].
故选A.
点评:本题考查Venn图表达集合的关系及运算,考查指数函数的定义、解析式、定义域和值域,理解图形含义是解题的关键,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
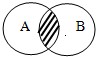 1、设A、B为非空集合,定义集合A*B为如图非阴影部分表示的集合,若A={x|y=
1、设A、B为非空集合,定义集合A*B为如图非阴影部分表示的集合,若A={x|y=| 2x-x2 |
| A、(0,2) |
| B、[0,1]∪[2,+∞) |
| C、(1,2] |
| D、[0,1]∪(2,+∞) |