Question

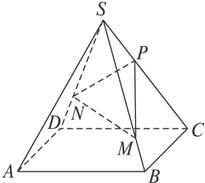
如图2-5,S是正方形ABCD所在平面外一点,且SA=SB=SC=SD,点P在SC上,满足SP∶PC=1∶2,又点M与N分别在SB和SD上,且BM=DN,求当MN∶BD的值为多少时,SA∥平面PMN？

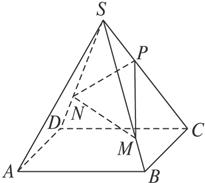
图2-5

Answer 1

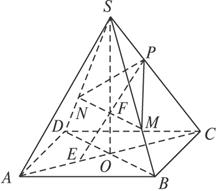
连结AC、BD,设AC与BD交于点O,连SO,并设SO∩MN=F,连PF并延长PF使PF∩AC=E.

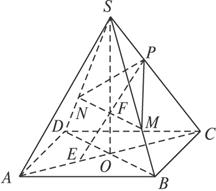
图2-6

∵SA∥平面PMN,面SAC∩面PMN=PE,

∴SA∥PE.

∴△SCA中,=.

∴=.

∴=2.

∴=2.

又∵BM=DN,SD=SB,

∴MN∥BD.

∴.

所以当MN∶BD=2∶3时,SA∥平面PMN.

解析:

选取截面SAC来研究问题.欲求当MN∶BD的值为多少时,SA∥平面PMN,这个问题可转化为求当SA∥平面PMN时,MN∶BD的值为多少.若SA∥平面PMN(线面平行),则先找线线平行的关系,有SA平行于平面PMN与面SAC的交线PE.