题目内容
已知双曲线的顶点与焦点分别是椭圆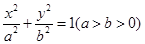 的焦点和顶点,若双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,则椭圆的离心率为( )
的焦点和顶点,若双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,则椭圆的离心率为( )
A. 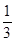 B.
B.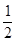 C.
C.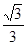 D.
D.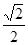
【答案】
D
【解析】
试题分析:设椭圆的焦点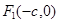 ,
, ,由题意可知双曲线方程为
,由题意可知双曲线方程为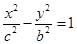 ,其渐近线方程为
,其渐近线方程为 ,又双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,所以由椭圆的对称性知双曲线的渐近线方程为
,又双曲线的两条渐近线与椭圆的焦点构成的四边形恰为正方形,所以由椭圆的对称性知双曲线的渐近线方程为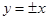 ,即
,即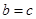 ,所以
,所以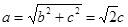 ,所以椭圆的离心率为
,所以椭圆的离心率为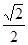 .
.
考点:双曲线、椭圆的性质,椭圆的离心率的求法.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 的方程为
的方程为  ,双曲线
,双曲线 的左、右焦
的左、右焦 与双曲线C2恒有两个不同的交点A和B,求
与双曲线C2恒有两个不同的交点A和B,求 的范围。
的范围。