题目内容

已知f（x）=x-1，g（x）=-x2+（3m+1）x-2m（m+1），满足下面两个条件：
①对任意实数x，有f（x）＜0或g（x）＜0；
②存在x∈（-∞，-2），满足f（x）•g（x）＜0．
则实数m的取值范围为（　　）
分析：当x≥1时，f（x）=x-1＜0不成立，所以要求当x≥1时g（x）＜0；只需g（x）max＜0求得结果记为A；当x∈（-∞，-2）时，f（x）＜0．需要存在x∈（-∞，-2），使g（x）＞0．只需g（x）max＞0，求得结果记为B，则最后结果为A∩B
解答：解：当x≥1时，f（x）=x-1＜0不成立，所以要求当x≥1时g（x）＜0；，所以
-
3m+1
-2
≤1
g(1)＜0
或
-
3m+1
-2
＞1
g(
3m+1
2
)＜0

得满足条件①m＜0
当x∈（-∞，-2）时，f（x）＜0．需要存在x∈（-∞，-2），使g（x）＞0．
（1）
-
3m+1
-2
≥-2
g(-2)≥0
得-
5
3
≤m≤-1
（2）
-
3m+1
-2
＜-2
g(
3m+1
2
)＞0
得m＜-
5
3

所以满足②的m范围为-
5
3
≤m≤-1或m＜-
5
3
，即m≤-1
综上所述，m范围为（-∞，0）∩（（-∞，-1）=（-∞，-1）
故选A
点评：本题考查不等式恒成立，函数最值的应用，考查逻辑思维能力，推理运算能力．
练习册系列答案
相关题目
已知函数f(
x
-1)=-x，则函数f（x）的表达式为（　　）
A、f（x）=x2+2x+1（x≥0）
B、f（x）=x2+2x+1（x≥-1）
C、f（x）=-x2-2x-1（x≥0）
D、f（x）=-x2-2x-1（x≥-1）
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-kx3．（k≥0）
（Ⅰ）求g（x）的解析式；
（Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
（Ⅲ）若k=
1
3
，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间[
1
2
，a]上的值域为[
1
a
，1]，若存在，求出a的值；若不存在，请说明理由．
已知f(x
1
2
+x-
1
2
)=x+x-1-2，则 f（x+1）=（　　）
已知f(x)=
x
+
1
x
+
x+
1
x
+1
及g(x)=
x
+
1
x
-
x+
1
x
+1
．
（1）分别求f（x）、g（x）的定义域，并求f（x）•g（x）的值；（2）求f（x）的最小值并说明理由；
（3）若a=
x2+x+1
 ， b=t
x
 ， c=x+1，是否存在满足下列条件的正数t，使得对于任意的正
数x，a、b、c都可以成为某个三角形三边的长？若存在，则求出t的取值范围；若不存在，请说明理由．
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-kx3．（k≥0）
（Ⅰ）求g（x）的解析式；
（Ⅱ）讨论函数f（x）在区间（-∞，0）上的单调性；
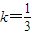（Ⅲ）若，设g（x）是函数f（x）在区间[0，+∞）上的导函数，问是否存在实数a，满足a＞1并且使g（x）在区间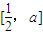上的值域为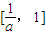，若存在，求出a的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网