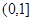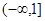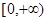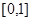题目内容
已知集合M="{y|y" =x2+1,x∈R},N="{y|y" =x+1,x∈R},则M∩N=( )
| A.(0,1),(1,2) | B.{(0,1),(1,2)} |
| C.{y|y=1,或y=2} | D.{y|y≥1} |
D
【错解分析】求M∩N及解方程组
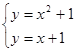 得
得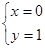 或
或 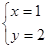 ∴选B
∴选B【正解】M={y|y=x2+1,x∈R}={y|y≥1}, N={y|y=x+1,x∈R}={y|y∈R}.
∴M∩N={y|y≥1}∩{y|(y∈R)}={y|y≥1}, ∴应选D.
【点评】集合是由元素构成的,认识集合要从认识元素开始,要注意区分{x|y=x2+1}、{y|y=x2+1,x∈R}、{(x,y)|y=x2+1,x∈R},这三个集合是不同的.

练习册系列答案
相关题目
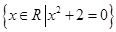
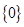
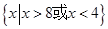
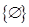
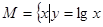
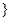 ,集合
,集合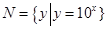 ,则( )
,则( )
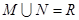

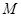

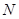
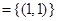
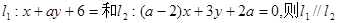 的充要条件是
的充要条件是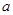 = .
= .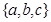 的非空子集个数为( )
的非空子集个数为( )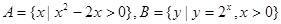 ,
,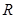 是实数集,则
是实数集,则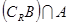 等于( )
等于( )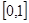
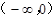
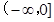
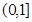
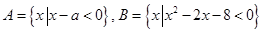 .
.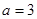 ,全集
,全集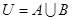 ,求
,求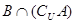 ;
;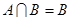 ,求实数
,求实数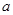 的取值范围.
的取值范围.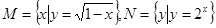 ,则
,则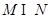 ="(" )
="(" )