题目内容
一个球从100m高处落下,每次着地后又跳回到原高度的一半再落下.(1)当它第6次着地时,经过的路程共有多少?
(2)当它第n次着地时,经过的路程是多少?
【答案】分析:(1)因为第1次小球下落到地面球经过的路程为100米,第2次开始球经过的路程为来回路程,根据每次着地后又跳回到原高度的一半再落下,得到第二次经过的路程为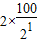 ;第3次经过的路程为2×
;第3次经过的路程为2×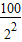 ;同理可得第4、5、6次球经过的路程,表示出六次经过的路程之和,然后利用等比数列的前n项和的公式化简可得;
;同理可得第4、5、6次球经过的路程,表示出六次经过的路程之和,然后利用等比数列的前n项和的公式化简可得;
(2)根据(1)得到等比数列的首项和公比,然后利用等比数列的前n项和的公式表示出第n次着地经过的路程即可.
解答:解:(1)100+2(50+25+…+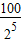 )=100+200(1-
)=100+200(1-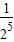 )=300-
)=300-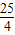 =
=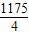 =293.75;
=293.75;
(2)100+2×100[2-1+2-2+…+2-(n-1)]=300-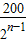 .
.
答:当球第6次着地时,经过的路程共有293.75;当球第n次着地时,经过的路程是300-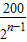 .
.
点评:本题考查了等比数列的前n项和的公式,考查学生根据条件归纳总结的能力.
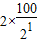 ;第3次经过的路程为2×
;第3次经过的路程为2×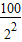 ;同理可得第4、5、6次球经过的路程,表示出六次经过的路程之和,然后利用等比数列的前n项和的公式化简可得;
;同理可得第4、5、6次球经过的路程,表示出六次经过的路程之和,然后利用等比数列的前n项和的公式化简可得;(2)根据(1)得到等比数列的首项和公比,然后利用等比数列的前n项和的公式表示出第n次着地经过的路程即可.
解答:解:(1)100+2(50+25+…+
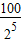 )=100+200(1-
)=100+200(1-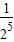 )=300-
)=300-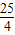 =
=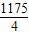 =293.75;
=293.75;(2)100+2×100[2-1+2-2+…+2-(n-1)]=300-
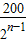 .
.答:当球第6次着地时,经过的路程共有293.75;当球第n次着地时,经过的路程是300-
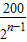 .
.点评:本题考查了等比数列的前n项和的公式,考查学生根据条件归纳总结的能力.

练习册系列答案
相关题目