题目内容
9.已知数列{an}是递增的等比数列,a1+a4=9,a2a3=8,则a6的值等于32.分析 数列{an}是递增的等比数列,a1+a4=9,a2a3=8=a1a4,解得a1,a4.再利用等比数列的通项公式即可得出.
解答 解:∵数列{an}是递增的等比数列,a1+a4=9,a2a3=8=a1a4,
解得a1=1,a4=8.
∴q3=8,解得q=2.
∴a6=25=32.
故答案为:32.
点评 本题考查了等比数列的通项公式、一元二次方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知焦点在y轴上的双曲线C的一条渐近线与直线$l:x+\sqrt{3}y=0$垂直,且C的一个焦点到l的距离为3,则C的标准方程为( )
| A. | $\frac{y^2}{9}-\frac{x^2}{3}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{3}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{6}=1$ | D. | $\frac{x^2}{4}-\frac{y^2}{6}=1$ |
17.如图所示的一个几何体及其正视图如图,则其俯视图是( )
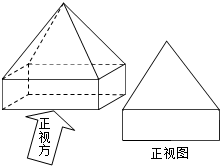

| A. |  | B. | 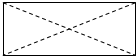 | C. | 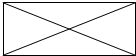 | D. | 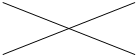 |
1.已知命题p:?x>0,总有(x+1)ex>1,则¬p为( )
| A. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | B. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | ||
| C. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | D. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 |
18.在△ABC中,a=$\sqrt{3}$,b=2,c=1,那么角A的值是( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |