题目内容
如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。
(1)求证:EF//平面PAD;
(2)求证:EF⊥CD;
(3)若∠PDA=450,求EF与平面ABCD所成的角的大小
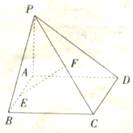
(3)EF与平面ABCD所成角450…
解析:
(1)取PD中点Q,连AQ、QF,则AE//QF
∴四边形AEFQ为平行四边形
∴EF//AQ
又∵AQ在平面PAD内,EF不在平面PAD内
∴EF//面PAD……………………………………4分
(2)证明∵CD⊥AD CD⊥PA PA ∩AD=A
PA在平面PAD内,AD在平面PAD内
∴CD⊥面PAD
又∵AQ在平面PAD同
∴CD⊥AQ
∵EF//AQ
∴CD⊥EF………………………………………8分
(3)解∵∠PDA=450
∴△PAD为等腰直角三角形
∴AQ⊥PD
∴∠QAD=450
即AQ与平面ABCD所成角为450
又∵AQ//EF
∴EF与平面ABCD所成角450……………………13分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
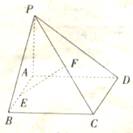 (13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。
(13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。 (13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。
(13分)如图3,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB,PC的中点。