题目内容
设 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集为( )
的解集为( )
A. B.
B.
C. D.
D.
【答案】
D
【解析】
试题分析:不等式 的解集等价于不等式
的解集等价于不等式 的解集。令
的解集。令 ,由于当
,由于当 时,有
时,有 恒成立,则
恒成立,则 ,所以函数
,所以函数 在
在 上是减函数,又
上是减函数,又 ,则
,则 ,又由于
,又由于 是定义在R上的奇函数,即有
是定义在R上的奇函数,即有 ,则函数
,则函数 满足
满足 ,是偶函数。画出函数
,是偶函数。画出函数 的图像如下,则不等式
的图像如下,则不等式 的解集为
的解集为 。故选D。
。故选D。

考点:不等式的解集
点评:求不是具体不等式的解集,常通过画出函数的图像,然后从图像得到不等式的解集。

练习册系列答案
相关题目
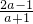 ,则a的取值范围是________.
,则a的取值范围是________. ,则a的取值范围是 .
,则a的取值范围是 .