题目内容
动点M(x,y)到定点F(-1,0)的距离与到y轴的距离之差为1.(I)求动点M的轨迹C的方程;
(II)过点Q(-3,0)的直线l与曲线C交于A、B两点,问直线x=3上是否存在点P,使得△PAB是等边三角形?若存在,求出所有的点P;若不存在,请说明理由.
【答案】分析:(I)利用动点M(x,y)到定点F(-1,0)的距离与到y轴的距离之差为1,建立方程,化简方程可得M点的轨迹方程;
(II)设l的方程为x=my-3,代入y2=-4x,消元可得y2+4my-12=0,利用韦达定理,可得|AB|,结合△PAB是等边三角形得:PM⊥AB且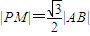 ,由此可得结论.
,由此可得结论.
解答:解:(I)依题意有: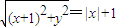 …(2分)
…(2分)
当x≥0时,y=0;当x<0时,y2=-4x…(5分)
∴M点的轨迹方程为 …(6分)
…(6分)
(II)由题意,l只能与抛物线y2=-4x相交.
设l的方程为x=my-3,代入y2=-4x,消元可得y2+4my-12=0…(7分)
设A(x1,y1)B(x2,y2)则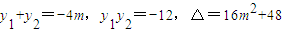
∴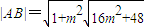 …(8分)
…(8分)
AB的中点M(-2m2-3,-2m)
由△PAB是等边三角形得:PM⊥AB且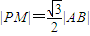 …(9分)
…(9分)
令点P(3,n)则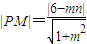 …(10分)
…(10分)
∴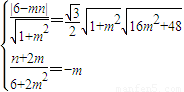 ,解得
,解得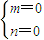
所以存在点P(3,0)使得△PAB是等边三角形.…(13分)
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.
(II)设l的方程为x=my-3,代入y2=-4x,消元可得y2+4my-12=0,利用韦达定理,可得|AB|,结合△PAB是等边三角形得:PM⊥AB且
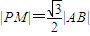 ,由此可得结论.
,由此可得结论.解答:解:(I)依题意有:
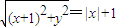 …(2分)
…(2分)当x≥0时,y=0;当x<0时,y2=-4x…(5分)
∴M点的轨迹方程为
 …(6分)
…(6分)(II)由题意,l只能与抛物线y2=-4x相交.
设l的方程为x=my-3,代入y2=-4x,消元可得y2+4my-12=0…(7分)
设A(x1,y1)B(x2,y2)则
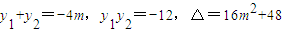
∴
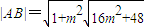 …(8分)
…(8分)AB的中点M(-2m2-3,-2m)
由△PAB是等边三角形得:PM⊥AB且
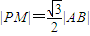 …(9分)
…(9分)令点P(3,n)则
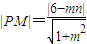 …(10分)
…(10分)∴
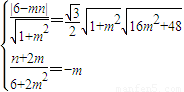 ,解得
,解得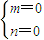
所以存在点P(3,0)使得△PAB是等边三角形.…(13分)
点评:本题考查轨迹方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
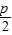 ,0),(p>0)定直线l:x=
,0),(p>0)定直线l:x=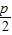 ,动点M(x,y)到定点的距离等于到定直线l的距离.
,动点M(x,y)到定点的距离等于到定直线l的距离.