题目内容
已知定点F(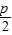 ,0),(p>0)定直线l:x=
,0),(p>0)定直线l:x=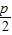 ,动点M(x,y)到定点的距离等于到定直线l的距离.
,动点M(x,y)到定点的距离等于到定直线l的距离.(Ⅰ)求动点M的轨迹方程;
(Ⅱ)动点M的轨迹上的点到直线3x+4y+12=0的距离的最小值为1,求p的值.
【答案】分析:(1)根据题意可得: =|x+
=|x+ |,两边平方即可求动点M的轨迹方程;
|,两边平方即可求动点M的轨迹方程;
(2)设A(x,y)为抛物线y2=2px,(p>0)上任意一点,则A到直线3x+4y+12=0的距离为d,利用dmin=1可得到关于p的不等式,解之即可.
解答:解:(1)∵定点F(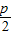 ,0)(p>0),定直线l:x=-
,0)(p>0),定直线l:x=- ,动点M(x,y)到定点的距离等于到定直线l的距离,
,动点M(x,y)到定点的距离等于到定直线l的距离,
∴ =|x+
=|x+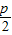 |,
|,
∴动点M的轨迹方程为y2=2px,(p>0)(4分)
(2)将直线3x+4y+12=0平移到与曲线y2=2px(p>0)相切,切点设为A(x,y),
则A到直线3x+4y+12=0的距离为1.设切线方程为:3x+4y+t=0,
由 消去x得:3y2+8py+2pt=0,
消去x得:3y2+8py+2pt=0,
△=64p2-4×3×2pt=0,p>0,
∴t= p…(6分)
p…(6分)
∴点A到直线3x+4y+12=0的距离就是两平行线3x+4y+12=0与3x+4y+t=0的距离,为1,
∴d= =
=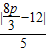 =1,
=1,
∴p=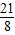 或p=
或p= …(12分)
…(12分)
点评:本题考查直线与圆锥曲线的关系,着重考查抛物线的定义及其应用与配方法求最值,属于难题.
 =|x+
=|x+ |,两边平方即可求动点M的轨迹方程;
|,两边平方即可求动点M的轨迹方程;(2)设A(x,y)为抛物线y2=2px,(p>0)上任意一点,则A到直线3x+4y+12=0的距离为d,利用dmin=1可得到关于p的不等式,解之即可.
解答:解:(1)∵定点F(
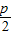 ,0)(p>0),定直线l:x=-
,0)(p>0),定直线l:x=- ,动点M(x,y)到定点的距离等于到定直线l的距离,
,动点M(x,y)到定点的距离等于到定直线l的距离,∴
 =|x+
=|x+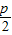 |,
|,∴动点M的轨迹方程为y2=2px,(p>0)(4分)
(2)将直线3x+4y+12=0平移到与曲线y2=2px(p>0)相切,切点设为A(x,y),
则A到直线3x+4y+12=0的距离为1.设切线方程为:3x+4y+t=0,
由
 消去x得:3y2+8py+2pt=0,
消去x得:3y2+8py+2pt=0,△=64p2-4×3×2pt=0,p>0,
∴t=
 p…(6分)
p…(6分)∴点A到直线3x+4y+12=0的距离就是两平行线3x+4y+12=0与3x+4y+t=0的距离,为1,
∴d=
 =
=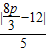 =1,
=1,∴p=
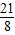 或p=
或p= …(12分)
…(12分)点评:本题考查直线与圆锥曲线的关系,着重考查抛物线的定义及其应用与配方法求最值,属于难题.

练习册系列答案
相关题目
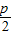 ,0),(p>0)定直线l:x=
,0),(p>0)定直线l:x=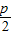 ,动点M(x,y)到定点的距离等于到定直线l的距离.
,动点M(x,y)到定点的距离等于到定直线l的距离.