Question

半径为10的球面上有A、B、C三点，AB=6，BC=8，CA=10，则球心O到平面ABC的距离是

 

．

Answer 1

分析：“AB=6，BC=8，CA=10”这是一个常用的直角三角形的长度组合，故AC即为A、B、C三点所在圆的直径，取AC的中点M，连接OM，则OM即为球心到平面ABC的距离，在Rt△OMA中，OA=10，MA=5，求出OM即可．

解答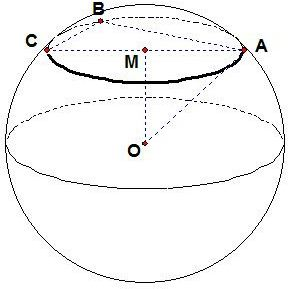：解：如图所示：
∵AB=6，BC=8，CA=10，
∴∠CBA=90°
∴取AC的中点M，则球面上A、B、C三点所在的圆即为⊙M，连接OM，则OM即为球心到平面ABC的距离，
在Rt△OMA中，OA=10，MA=5，
∴OM=5

3

，即球心到平面ABC的距离为5

3

．
故答案为：5

3

点评：本小题主要考查立体几何球面距离及点到面的距离．注意小圆与球心的关系．