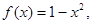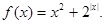题目内容
记具有如下性质的函数的集合为M:对任意的x1、x2∈R,若x12<x22,则f(x1)<f(x2),现给定函数①y=ln(|x|+1)②y=x2ex③y=x4+x3+1④y=
x2+cosx则上述函数中,属于集合M的函数序号是______.
| 1 |
| 2 |
①若x12<x22,则|x1|<|x2|,所以ln(|x1|+1)<ln(|x2|+1)即f(x1)<f(x2).所以①符合要求.
②令x1=-
,x2=-1,则x12<x22.所以f(x1)=
>f(x2)=
.所以②不符合要求.
③令x1=-
,x2=-
,则x12<x22.所以f(x1)=1-
>f(x2)=1-
.所以③不符合要求.
④由题意得y′=x+sinx,设f(x)=y′=x+sinx,所以f′(x)=1+cosx≥0恒成立,所以f(x)=y′=x+sinx是单调减函数.即得到当x>0时y′>0,当x<0时y′<0,所以当x>0时,y=
x2+cosx是增函数,当x<0时y=
x2+cosx是奇函数.
若x12<x22,则|x1|<|x2|,所以
|x1|2+cos|x1|<
|x2|2+cos|x2|,由函数是偶函数可得
x12+cos|x1|<
x22+cosx2.所以④符合要求.
故答案为:①④.
②令x1=-
| 1 |
| 2 |
| 1 | ||
|
| 1 |
| e |
③令x1=-
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 81 |
| 1 |
| 16 |
④由题意得y′=x+sinx,设f(x)=y′=x+sinx,所以f′(x)=1+cosx≥0恒成立,所以f(x)=y′=x+sinx是单调减函数.即得到当x>0时y′>0,当x<0时y′<0,所以当x>0时,y=
| 1 |
| 2 |
| 1 |
| 2 |
若x12<x22,则|x1|<|x2|,所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:①④.

练习册系列答案
相关题目
 、
、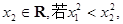 则
则 ,现给定函数①
,现给定函数①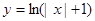 ②
②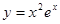 ③
③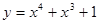
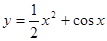
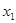 、
、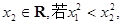 则
则 ,现给定函数①
,现给定函数① ②
②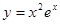 ③
③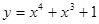
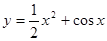
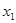 、
、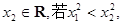 则
则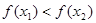 ,现给定函数①
,现给定函数①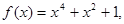 ②
②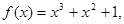 ③
③