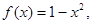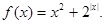题目内容
记具有如下性质的函数的集合为M:对任意的x1、x2∈R,若x12<x22,则f(x1)<f(x2),现给定函数
①f(x)=x4+x2+1,②f(x)=x3+x2+1,③f(x)=1-x2,④f(x)=x2+2|x|.
则上述函数中,属于集合M的函数序号是 .
①f(x)=x4+x2+1,②f(x)=x3+x2+1,③f(x)=1-x2,④f(x)=x2+2|x|.
则上述函数中,属于集合M的函数序号是
分析:由已知中函数的集合为M:对任意的x1、x2∈R,若x12<x22,则f(x1)<f(x2),我们可得满足条件的函数在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,逐一分析题目中四个函数的单调性,比照后,即可得到答案.
解答:解:对任意的x1、x2∈R,若x12<x22,则f(x1)<f(x2),
则函数在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增
①中,由f(x)=x4+x2+1,得f′(x)=4x3+2x,当x∈(-∞,0)时,f′(x)<0,当x∈(0,+∞)时,f′(x)>0,故①中函数符合条件;
②中,由f(x)=x3+x2+1,得f′(x)=3x2+2x,当x∈(-∞,0)时,f′(x)符号不确定,故②中函数不符合条件;
③中,由f(x)=1-x2,得f′(x)=-2x,当x∈(-∞,0)时,f′(x)>0,故③中函数不符合条件;
④f(x)=x2+2|x|,当x∈(0,+∞)时,f(x)=x2+2x为增函数,当x∈(-∞,0)时,f(x)=x2+
x为减函数,故④中函数符合条件;
故答案为:①④
则函数在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增
①中,由f(x)=x4+x2+1,得f′(x)=4x3+2x,当x∈(-∞,0)时,f′(x)<0,当x∈(0,+∞)时,f′(x)>0,故①中函数符合条件;
②中,由f(x)=x3+x2+1,得f′(x)=3x2+2x,当x∈(-∞,0)时,f′(x)符号不确定,故②中函数不符合条件;
③中,由f(x)=1-x2,得f′(x)=-2x,当x∈(-∞,0)时,f′(x)>0,故③中函数不符合条件;
④f(x)=x2+2|x|,当x∈(0,+∞)时,f(x)=x2+2x为增函数,当x∈(-∞,0)时,f(x)=x2+
| 1 |
| 2 |
故答案为:①④
点评:本题考查的知识点是元素与集合关系的判断,其中正确理解集合中元素所满足的性质,并将其转化为熟知的性质,如本题中将对任意的x1、x2∈R,若x12<x22,则f(x1)<f(x2),转化为函数在区间(-∞,0)上单调递减,在区间(0,+∞)上单调递增,是解答本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 、
、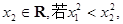 则
则 ,现给定函数①
,现给定函数①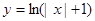 ②
②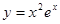 ③
③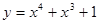
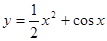
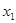 、
、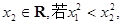 则
则 ,现给定函数①
,现给定函数① ②
②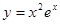 ③
③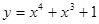
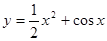
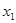 、
、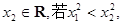 则
则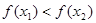 ,现给定函数①
,现给定函数①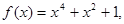 ②
②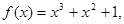 ③
③