题目内容
已知椭圆9x2+2y2=18上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且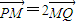 ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.(Ⅰ)求曲线E的方程;
(Ⅱ)若过定点F(0,2)的直线l交曲线E于不同的两点G,H(点G在点F,H之间),且满足
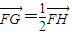 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(I)设点P(x,y)是椭圆上一点,则Q(x,0),M(x,y).由已知 得:x=x,y=3y代入椭圆方程即可得到曲线E的方程.
得:x=x,y=3y代入椭圆方程即可得到曲线E的方程.
(II)设G(x1,y1),H(x2,y2),当直线GH斜率存在时,设直线GH的斜率为k.把直线GH的方程y=kx+2与椭圆的方程联立,得到根与系数的关系,再利用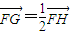 ,即可解出k.当直线GH斜率不存在时,不符合题意.
,即可解出k.当直线GH斜率不存在时,不符合题意.
解答:解:(I)设点P(x,y)是椭圆上一点,则Q(x,0),M(x,y)
由已知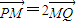 得:x=x,y=3y代入椭圆方程得9x2+18y2=18,
得:x=x,y=3y代入椭圆方程得9x2+18y2=18,
即x2+2y2=2为曲线E的方程.
(II)设G(x1,y1),H(x2,y2),
当直线GH斜率存在时,设直线GH的斜率为k
则直线GH的方程为:y=kx+2,
代入x2+2y2=2,得:( +k2)x2+4kx+3=0,
+k2)x2+4kx+3=0,
由△>0,解得:k2> ,
, ,
, ,
,
∵ ,
, ,又有
,又有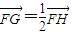 .
.
∴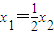
.∴
化为 ,即10k2=27.
,即10k2=27.
解得: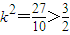 ,
,
∴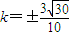 ,
,
∴直线l的方程为:y=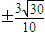 x+2,
x+2,
当直线GH斜率不存在时,直线的l方程为x=0,
此时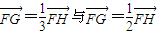 矛盾不合题意.
矛盾不合题意.
∴所求直线l的方程为:y= x+2.
x+2.
点评:熟练掌握直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量相等、分类讨论思想方法等是解题的关键.
 得:x=x,y=3y代入椭圆方程即可得到曲线E的方程.
得:x=x,y=3y代入椭圆方程即可得到曲线E的方程.(II)设G(x1,y1),H(x2,y2),当直线GH斜率存在时,设直线GH的斜率为k.把直线GH的方程y=kx+2与椭圆的方程联立,得到根与系数的关系,再利用
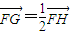 ,即可解出k.当直线GH斜率不存在时,不符合题意.
,即可解出k.当直线GH斜率不存在时,不符合题意.解答:解:(I)设点P(x,y)是椭圆上一点,则Q(x,0),M(x,y)
由已知
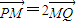 得:x=x,y=3y代入椭圆方程得9x2+18y2=18,
得:x=x,y=3y代入椭圆方程得9x2+18y2=18,即x2+2y2=2为曲线E的方程.
(II)设G(x1,y1),H(x2,y2),
当直线GH斜率存在时,设直线GH的斜率为k
则直线GH的方程为:y=kx+2,
代入x2+2y2=2,得:(
 +k2)x2+4kx+3=0,
+k2)x2+4kx+3=0,由△>0,解得:k2>
 ,
, ,
, ,
,∵
 ,
, ,又有
,又有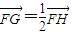 .
.∴
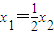
.∴

化为
 ,即10k2=27.
,即10k2=27.解得:
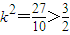 ,
,∴
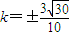 ,
,∴直线l的方程为:y=
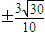 x+2,
x+2,当直线GH斜率不存在时,直线的l方程为x=0,
此时
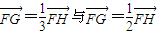 矛盾不合题意.
矛盾不合题意.∴所求直线l的方程为:y=
 x+2.
x+2.点评:熟练掌握直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量相等、分类讨论思想方法等是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目