题目内容
已知椭圆9x2+2y2=18上任意一点P,由P向x轴作垂线段PQ,垂足为Q,点M在线段PQ上,且![]() ,点M的轨迹为曲线E.
,点M的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若过定点F(0,2)的直线l交曲线E于不同的两点G,H(点G在点F,H之间),且满足![]() ,求直线l的方程.
,求直线l的方程.
答案:
解析:
解析:
|
解:(I)设点P(x0,y0),是椭圆上一点,则Q(x0,0),M(x,y) 由已知得:x0=x,y0=3y代入椭圆方程得 9x2+18y2=18即x2+2y2=2为曲线E的方程. 4分 (II)设G(x1,y1),H(x2,y2) 当直线GH斜率存在时,设直线GH的斜率为k 则直线GH的方程为:y=kx+2, 5分 代入x2+2y2=2,得:( 由△>0,解得:k2> ∴将(1)代入(2)整理得: 解得: ∴直线l的方程为:y= 当直线GH斜率不存在时,直线的l方程为x=0,此时 ∴所求直线l的方程为:y= |

练习册系列答案
相关题目
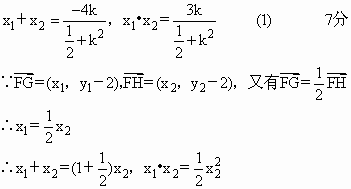
 (2)
(2) 9分
9分