题目内容
一个化肥厂生产甲、乙两种混合肥料，生产1车皮甲种肥料的主要原料是磷酸盐4t，硝酸盐18t；生产1车乙种肥料的主要原料是磷酸盐1t、硝酸盐15t。现库存磷酸盐10t、硝酸盐66t。已知生产1车皮甲种肥料，产生的利润为10000元；生产1车皮乙种肥料，产生的利润为5000元。那么分别生产甲、乙两种肥料各多少车皮，能够产生最大利润？最大利润是多少？
生产甲、乙两种肥料各2车皮，能够产生最大利润是3万元
根据题意列出线性约束条件，画图目标函数
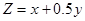中z看做直线
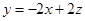在y轴上的截距，当过点M时，Z有最大值，带入点M坐标得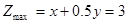
解：设生产甲种肥料x车皮，乙种肥料y车皮，能够产生利润Z万元……2分
则有：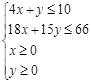
目标函数为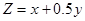 ………………6分
做出可行域如图所示
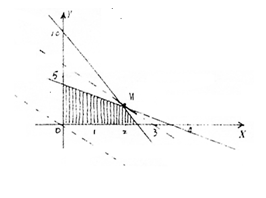
平移直线x + 0.5y = 0，当其过可行域上点M时，Z有最大值。……………………8分
解方程组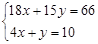
得M的坐标x = 2，y = 2 所以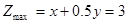
由此可知，生产甲、乙两种肥料各2车皮，能够产生最大利润是3万元
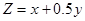中z看做直线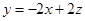在y轴上的截距，当过点M时，Z有最大值，带入点M坐标得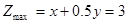解：设生产甲种肥料x车皮，乙种肥料y车皮，能够产生利润Z万元……2分
则有：
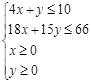
目标函数为
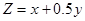………………6分做出可行域如图所示
平移直线x + 0.5y = 0，当其过可行域上点M时，Z有最大值。……………………8分
解方程组
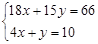得M的坐标x = 2，y = 2 所以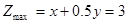 由此可知，生产甲、乙两种肥料各2车皮，能够产生最大利润是3万元
练习册系列答案
相关题目
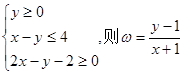的取值范围是（ ）
满足约束条件
则
的最大值为
则z=3x-y的最小值为_________.
、
及任意的
，当甲公司投入
万元作宣传时，若乙公司投入的宣传费小于
的实际意义；
时，甲、乙两公司为了避免恶性竞争，经过协商，同意在双方均无失败风险的情况下尽可能地少投入宣传费用，问此时甲、乙两公司应各投入多少宣传费用？
两个等级．对每种产品，两道工序的加工结果都为
级时，产品为一等品，其余均为二等品。
；
分别表示一件甲、乙产品的利润，在（1）的条件下，求
；
名，可用资金
万元。设
分别表示生产甲、乙产品的数量，在（2）的条件下，
最大？最大值是多少？（解答时须给出图示说明）
满足约束条件
,则
的最大值为（ ）
，最小值为 .