题目内容
已知抛物线C:y=ax2(a>0)上的点P(b,1)到焦点的距离为 ,
,(Ⅰ)求a的值;
(Ⅱ)如图,已知动线段AB(B在A右边)在直线l:y=x-2上,且
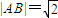 ,现过A作C的切线,取左边的切点M,过B作C的切线,取右边的切点为N,当MN∥AB,求A点的横坐标t的值.
,现过A作C的切线,取左边的切点M,过B作C的切线,取右边的切点为N,当MN∥AB,求A点的横坐标t的值.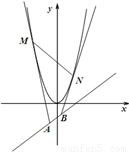
【答案】分析:(Ⅰ)求出抛物线的准线方程,利用抛物线的定义把点P(b,1)到焦点的距离转化为到准线的距离,由此可求a的值;
(Ⅱ)设出M和N的坐标,利用导数求出过M和N的切线方程,由t表示出A,B的坐标,把A,B代入切线方程后求出M和N的坐标,由两点式写出MN所在直线的斜率,由斜率等于1即可求出t的值.
解答:解:(Ⅰ)抛物线C:y=ax2即 ,准线方程为:
,准线方程为: ,
,
∵点P(b,1)到焦点的距离为 ,∴
,∴ ,∴a=1,∴抛物线C的方程为y=x2;
,∴a=1,∴抛物线C的方程为y=x2;
(Ⅱ)设 ,∵y=x2,∴y'=2x,∴kAM=2x1,
,∵y=x2,∴y'=2x,∴kAM=2x1,
∴切线AM的方程为: ,即
,即 ,
,
同理可得切线BN的方程为:
由于动线段AB(B在A右边)在直线l:y=x-2上,且 ,
,
故可设A(t,t-2),B(t+1,t-1),
将A(t,t-2)代入切线AM的方程,得 ,即
,即 ,
,
∴ ,
,
同理可得 ,
,
∵ ,当MN∥AB时,kMN=1,得x1+x2=1,
,当MN∥AB时,kMN=1,得x1+x2=1,
∴
 ,
,
∴ ,
,
∴
得t=0或
 (舍去),∴t=0.
(舍去),∴t=0.
点评:本题考查了抛物线的方程,运用了数学转化思想方法.考查了直线与圆锥曲线的关系,训练了利用导数求曲线上某点的切线方程,考查了二次方程根的求法,解答此题的关键是用A点的坐标表示出B点的坐标,属难题.
(Ⅱ)设出M和N的坐标,利用导数求出过M和N的切线方程,由t表示出A,B的坐标,把A,B代入切线方程后求出M和N的坐标,由两点式写出MN所在直线的斜率,由斜率等于1即可求出t的值.
解答:解:(Ⅰ)抛物线C:y=ax2即
 ,准线方程为:
,准线方程为: ,
,∵点P(b,1)到焦点的距离为
 ,∴
,∴ ,∴a=1,∴抛物线C的方程为y=x2;
,∴a=1,∴抛物线C的方程为y=x2;(Ⅱ)设
 ,∵y=x2,∴y'=2x,∴kAM=2x1,
,∵y=x2,∴y'=2x,∴kAM=2x1,∴切线AM的方程为:
 ,即
,即 ,
,同理可得切线BN的方程为:

由于动线段AB(B在A右边)在直线l:y=x-2上,且
 ,
,故可设A(t,t-2),B(t+1,t-1),
将A(t,t-2)代入切线AM的方程,得
 ,即
,即 ,
,∴
 ,
,同理可得
 ,
,∵
 ,当MN∥AB时,kMN=1,得x1+x2=1,
,当MN∥AB时,kMN=1,得x1+x2=1,∴

 ,
,∴
 ,
,∴

得t=0或

 (舍去),∴t=0.
(舍去),∴t=0.点评:本题考查了抛物线的方程,运用了数学转化思想方法.考查了直线与圆锥曲线的关系,训练了利用导数求曲线上某点的切线方程,考查了二次方程根的求法,解答此题的关键是用A点的坐标表示出B点的坐标,属难题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
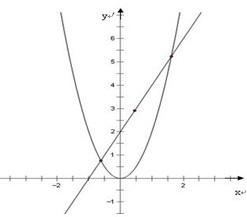 已知抛物线C:y=mx2(m>0),焦点为F,直线2x-y+2=0交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q,
已知抛物线C:y=mx2(m>0),焦点为F,直线2x-y+2=0交抛物线C于A、B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q, 已知抛物线C:y=ax2(a>0)上的点P(b,1)到焦点的距离为
已知抛物线C:y=ax2(a>0)上的点P(b,1)到焦点的距离为