题目内容
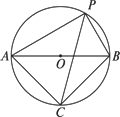
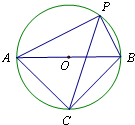已知如图，点A，P，B在⊙O上，∠APB=90°，PC平分∠APB，交⊙O于点C．求证：△ABC为等腰直角三角形．分析：利用圆的直径的性质、同圆中等弧所对的圆周角相等、角平分线的性质即可得出．
解答：证明：由∠APB=90°得AB为直径，∴∠ACB=90°．
由AC=AC，得∠APC=∠ABC，同理∠BPC=∠BAC．
又∵PC平分∠APB，∴∠CPA=∠CPB．
∴∠BAC=∠ABC，故BC=AC．
∴△ABC为等腰直角三角形．
由AC=AC，得∠APC=∠ABC，同理∠BPC=∠BAC．
又∵PC平分∠APB，∴∠CPA=∠CPB．
∴∠BAC=∠ABC，故BC=AC．
∴△ABC为等腰直角三角形．
点评：熟练掌握圆的直径的性质、同圆中等弧所对的圆周角相等、角平分线的性质等是解题的关键．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
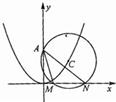已知如图，圆C的圆心在抛物线x2=2py（p＞0）上运动，且圆C过A（0，p）点，若MN为圆C在x轴上截得的弦．
已知如图，抛物线y=ax2+bx+2与x轴的交点是A（3，0）、B（6，0），与y轴的交点是C．
如图，点A、B是单位圆上的两点，A、B点分别在第一、二象限，点C是圆与x轴正半轴的交点，若∠COA=60°∠AOB=α，点B的坐标为