题目内容
若正三棱锥底面边长为1,侧棱与底面所成的角为
,则其体积为______.
| π |
| 4 |
先求正三棱锥的高,由题意,顶点P在底面中的射影是底面的中心O,
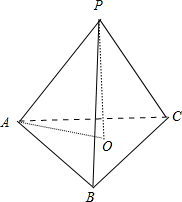
∠PAO为侧棱与底面所成角,∠PAO=45°,
从而有高PO=OA=
×
×1=
又底面积S△ABC=
×1×1=
∴正三棱锥的体积V=
×
×
=
故答案为:

∠PAO为侧棱与底面所成角,∠PAO=45°,
从而有高PO=OA=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
又底面积S△ABC=
| ||
| 4 |
| ||
| 4 |
∴正三棱锥的体积V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 1 |
| 12 |
故答案为:
| 1 |
| 12 |

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
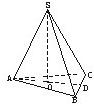 若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于
若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于
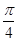 ,则其体积为____________。
,则其体积为____________。