题目内容
若正三棱锥底面边长为1,侧棱与底面所成的角为
,则其体积为
.
| π |
| 4 |
| 1 |
| 12 |
| 1 |
| 12 |
分析:欲求正三棱锥的体积,先求正三棱锥的高,由题意,顶点在底面中的射影是底面的中心,从而利用侧棱与底面所成角为45°角,可求高,从而得解
解答:解:先求正三棱锥的高,由题意,顶点P在底面中的射影是底面的中心O,
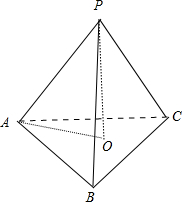
∠PAO为侧棱与底面所成角,∠PAO=45°,
从而有高PO=OA=
×
×1=
又底面积S△ABC=
×1×1=
∴正三棱锥的体积V=
×
×
=
故答案为:

∠PAO为侧棱与底面所成角,∠PAO=45°,
从而有高PO=OA=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
又底面积S△ABC=
| ||
| 4 |
| ||
| 4 |
∴正三棱锥的体积V=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 1 |
| 12 |
故答案为:
| 1 |
| 12 |
点评:本题主要考查棱锥,线面关系、直线与平面所成的角、点到面的距离等基本知识,同时考查空间想象能力和推理、运算能力.在立体几何中,求点到平面的距离是一个常见的题型,同时求直线到平面的距离、平行平面间的距离及多面体的体积也常转化为求点到平面的距离.

练习册系列答案
相关题目
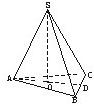 若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于
若正三棱锥底面边长为4,体积为1,则侧面和底面所成二面角的大小等于
 ,则其体积为____________。
,则其体积为____________。