题目内容
若圆x2+y2=4上存在与点（2a，a+3）距离为1的点，则a的取值范围为 ．
【答案】分析：由题意得，点（2a，a+3）到圆心（0，0）的距离大于或等于1小于或等于3，解一元二次不等式组求得a的取值范围．
解答：解：由题意得，点（2a，a+3）到圆心（0，0）的距离大于或等于1小于或等于3，
即 1≤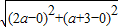
≤3，∴1≤5a2+6a+9≤9，
∴9≥5a2+6a≥-8，解得-
≤a≤0，
故答案为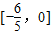
．
点评：本题考查点与圆的位置关系，两点间的距离公式的应用，一元二次不等式的解法，判断点（2a，a+3）到圆心（0，0）的距离大于或等于1小于或等于3，是解题的关键．
解答：解：由题意得，点（2a，a+3）到圆心（0，0）的距离大于或等于1小于或等于3，
即 1≤
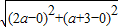≤3，∴1≤5a2+6a+9≤9，∴9≥5a2+6a≥-8，解得-
≤a≤0，故答案为
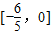．点评：本题考查点与圆的位置关系，两点间的距离公式的应用，一元二次不等式的解法，判断点（2a，a+3）到圆心（0，0）的距离大于或等于1小于或等于3，是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
，则所得曲线的方程是（ ）
的直线l的斜率为k，若圆x2+y2=4上恰有三点到直线l的距离等于1，则k的值是 ．