题目内容
(1)请填表
(2)根据表中数据填空:若n∈N*,则当
(3)证明在(2)中你所得的结论;
(4)若x∈R,猜想方程x2=2x有几个实数根?并简单说明猜想的过程.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| n2 | ||||||||
| 2n |
n=1或n≥5
n=1或n≥5
时,n2<2n;(3)证明在(2)中你所得的结论;
(4)若x∈R,猜想方程x2=2x有几个实数根?并简单说明猜想的过程.
分析:(1)根据函数表达式直接计算即可;
(2)可根据(1)所填的表格,结合指数函数与幂函数的性质观察后即可得到结论;
(3)用数学归纳法①n≥n0(n0=5)时成立,②假设n=k(k≥5)时成立,去证n=k+1时成立;
(4)由(1)中的表格及指数函数y=2x与幂函数y=x2的图象观察后即可得到结论.
(2)可根据(1)所填的表格,结合指数函数与幂函数的性质观察后即可得到结论;
(3)用数学归纳法①n≥n0(n0=5)时成立,②假设n=k(k≥5)时成立,去证n=k+1时成立;
(4)由(1)中的表格及指数函数y=2x与幂函数y=x2的图象观察后即可得到结论.
解答:解:(1)填表 …(2分)
(2)n=1或n≥5时 …(4分)
(少“n=1”扣1分)
(3)当n=5时,n2<2n成立 …(5分)
假设n=k(k≥5)时,k2<2k …(6分)
则当n=k+1时,2k+1=2•2k>2•k2 …(8分)
∵k>4,∴k2>4k=2k+2k>2k+1 …(10分)
∴2k+1>2•k2=k2+k2>k2+2k+1=(k+1)2,即(k+1)2<2k+1
当n=k+1时,n2<2n也成立 …(11分)
综上所述,当n≥5时,n2<2n成立 …(12分)
(4)有3个实数根 …(14分)
由表可知,有两整数根,由图象可知,还有一个负实根 …(16分)
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| n2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 |
(少“n=1”扣1分)
(3)当n=5时,n2<2n成立 …(5分)
假设n=k(k≥5)时,k2<2k …(6分)
则当n=k+1时,2k+1=2•2k>2•k2 …(8分)
∵k>4,∴k2>4k=2k+2k>2k+1 …(10分)
∴2k+1>2•k2=k2+k2>k2+2k+1=(k+1)2,即(k+1)2<2k+1
当n=k+1时,n2<2n也成立 …(11分)
综上所述,当n≥5时,n2<2n成立 …(12分)
(4)有3个实数根 …(14分)
由表可知,有两整数根,由图象可知,还有一个负实根 …(16分)
点评:本题考查数列的性质,易错点在于环节不全,考虑不周,(2)中少“n=1”,重点考查学生对数学归纳法的应用与数形结合思想的掌握,难点在于数学归纳法中放缩法的应用.

练习册系列答案
相关题目
已知函数f(x)=
,令g(x)=f(
).
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
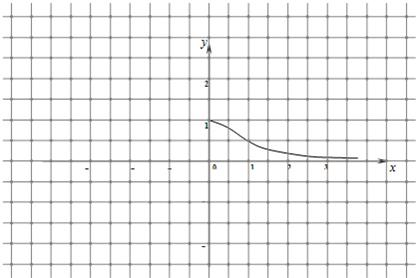
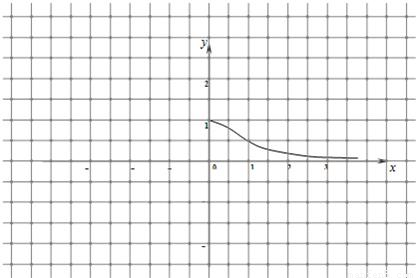
(3)如图,已知f(x)在区间[0,+∞)的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,并在同一坐标系中作出函数g(x)的图象.请说明你的作图依据.
| 1 |
| x2+1 |
| 1 |
| x |
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||||
f(x)-
|
… | |||||||
g(x)-
|
… |

已知函数 ,令
,令 .
.
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
(3)如图,已知f(x)在区间[0,+∞)的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,并在同一坐标系中作出函数g(x)的图象.请说明你的作图依据.

 ,令
,令 .
.(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||
 | … | |||||
 | … |

已知函数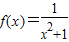 ,令
,令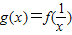 .
.
(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
(3)如图,已知f(x)在区间[0,+∞)的图象,请据此在该坐标系中补全函数f(x)在定义域内的图象,并在同一坐标系中作出函数g(x)的图象.请说明你的作图依据.
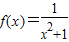 ,令
,令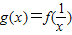 .
.(1)求函数f(x)的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
| x | … | |||||
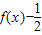 | … | |||||
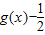 | … |

已知函数 ,令
,令 。
。
(1)求函数 的值域;
的值域;
(2)任取定义域内的5个自变量,根据要求计算并填表;观察表中数据间的关系,猜想一个等式并给予证明;
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
(3)如图,已知 在区间
在区间 的图像,请据此在该坐标系中补全函数
的图像,请据此在该坐标系中补全函数 在定义域内的图像,并在同一坐标系中作出函数
在定义域内的图像,并在同一坐标系中作出函数 的图像. 请说明你的作图依据.
的图像. 请说明你的作图依据.


