题目内容
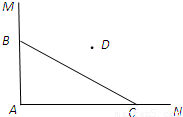
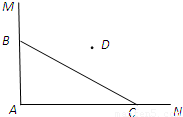
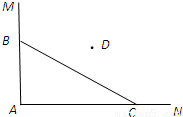
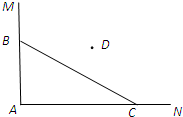 在一个矩形体育馆的一角MAN内(如图所示),用长为a的围栏设置一个运动器材储存区域,已知B是墙角线AM上的一点,C是墙角线AN上的一点.
在一个矩形体育馆的一角MAN内(如图所示),用长为a的围栏设置一个运动器材储存区域,已知B是墙角线AM上的一点,C是墙角线AN上的一点.(1)若BC=a=10,求储存区域三角形ABC面积的最大值;
(2)若AB=AC=10,在折线MBCN内选一点D,使DB+DC=a=20,求储存区域四边形DBAC面积的最大值.
分析:(1)设AC=x,AB=y,(x,y为正数),由勾股定理可得x2+y2=102=100,而三角形ABC的面积为:
xy,由基本不等式可得
xy≤
•
=25.
(2)只考虑三角形BCD的面积变化,点D的轨迹是一个椭圆,B、C是其焦点,结合椭圆的知识得结果.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2+y2 |
| 2 |
(2)只考虑三角形BCD的面积变化,点D的轨迹是一个椭圆,B、C是其焦点,结合椭圆的知识得结果.
解答:解:(1)设AC=x,AB=y,(x,y为正数),由勾股定理可得x2+y2=102=100,
而三角形ABC的面积为:
xy,由基本不等式可得
xy≤
•
=25
当且仅当x=y,即AB=AC时,三角形ABC的面积取最大值25
(2)因为四边形DBAC面积可分为ABC跟BCD两个三角形来计算,而ABC面积为定值可先不考虑,
故只考虑三角形BCD的面积变化,以BC为底边,故当D点BC 的距离最长时面积取得最大值.
因为DB+DC=a=20总成立,所以点D的轨迹是一个椭圆,B、C是其焦点,
结合椭圆的知识可以知道只有当D点在BC的中垂线上时点D到BC的距离才能取得最大值,
再结合题意四边形DBAC刚好是一个边长为10的正方形,
故其面积最大值为:100.
而三角形ABC的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2+y2 |
| 2 |
当且仅当x=y,即AB=AC时,三角形ABC的面积取最大值25
(2)因为四边形DBAC面积可分为ABC跟BCD两个三角形来计算,而ABC面积为定值可先不考虑,
故只考虑三角形BCD的面积变化,以BC为底边,故当D点BC 的距离最长时面积取得最大值.
因为DB+DC=a=20总成立,所以点D的轨迹是一个椭圆,B、C是其焦点,
结合椭圆的知识可以知道只有当D点在BC的中垂线上时点D到BC的距离才能取得最大值,
再结合题意四边形DBAC刚好是一个边长为10的正方形,
故其面积最大值为:100.
点评:本题为基本不等式和椭圆知识的结合,数列掌握基本不等式和椭圆的定义是解决问题关键,属中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
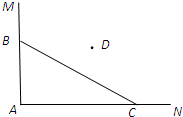 在一个矩形体育馆的一角MAN内(如图所示),用长为a的围栏设置一个运动器材储存区域,已知B是墙角线AM上的一点,C是墙角线AN上的一点.
在一个矩形体育馆的一角MAN内(如图所示),用长为a的围栏设置一个运动器材储存区域,已知B是墙角线AM上的一点,C是墙角线AN上的一点.