题目内容
已知向量 ,
, ,若存在正数k和t,使得向量
,若存在正数k和t,使得向量 与
与 互相垂直,则k的最小值是 .
互相垂直,则k的最小值是 .
【答案】分析:先求出 和
和  的坐标,根据两个平面向量垂直的性质可得
的坐标,根据两个平面向量垂直的性质可得  =0,化简可得 k=t+
=0,化简可得 k=t+ ,再利用基本不等式求得k的最小值.
,再利用基本不等式求得k的最小值.
解答:解:由题意可得 =(1-
=(1-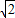 t2-
t2- ,
, +t2+1),
+t2+1), =(-k-
=(-k- ,-
,- k+
k+ ).
).
∵ ,∴
,∴ =(1-
=(1- t2-
t2- )(-k-
)(-k- )+(
)+( +t2+1)(-
+t2+1)(- k+
k+ )=-3(k-t-
)=-3(k-t- )=0,
)=0,
∴k=t+ ≥2,当且仅当t=1时,取等号,故k的最小值为2,
≥2,当且仅当t=1时,取等号,故k的最小值为2,
故答案为2.
点评:本题考查两个平面向量垂直的性质,基本不等式的应用,两个向量坐标形式的运算,考查运算求解能力,推理论证能力;考查化归与转化思想,对数学思维的要求比较高,
属于中档题.
 和
和  的坐标,根据两个平面向量垂直的性质可得
的坐标,根据两个平面向量垂直的性质可得  =0,化简可得 k=t+
=0,化简可得 k=t+ ,再利用基本不等式求得k的最小值.
,再利用基本不等式求得k的最小值.解答:解:由题意可得
 =(1-
=(1-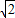 t2-
t2- ,
, +t2+1),
+t2+1), =(-k-
=(-k- ,-
,- k+
k+ ).
).∵
 ,∴
,∴ =(1-
=(1- t2-
t2- )(-k-
)(-k- )+(
)+( +t2+1)(-
+t2+1)(- k+
k+ )=-3(k-t-
)=-3(k-t- )=0,
)=0,∴k=t+
 ≥2,当且仅当t=1时,取等号,故k的最小值为2,
≥2,当且仅当t=1时,取等号,故k的最小值为2,故答案为2.
点评:本题考查两个平面向量垂直的性质,基本不等式的应用,两个向量坐标形式的运算,考查运算求解能力,推理论证能力;考查化归与转化思想,对数学思维的要求比较高,
属于中档题.

练习册系列答案
相关题目
 ,
, (n为正整数),函数
(n为正整数),函数 ,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.
,设f(x)在(0,+∞)上取最小值时的自变量x取值为an. ;
; ,
, (n为正整数),函数
(n为正整数),函数 ,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.
,设f(x)在(0,+∞)上取最小值时的自变量x取值为an. ;
; ,
, (n为正整数),函数
(n为正整数),函数 ,设f(x)在(0,+∞)上取最小值时的自变量x取值为an.
,设f(x)在(0,+∞)上取最小值时的自变量x取值为an. ;
;