题目内容
某种电子玩具按下按健后,会出现红球和绿球.已知按键第一按下后,出现红球和绿球的概率都是| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 3 |
| 5 |
| 2 |
| 5 |
(1)求p2;
(2)n≥2时,求pn.
分析:(1)根据题意,p2即第2次按下按键后出现红球的概率,分析可得,其包括第一次出现红球与绿球2种情况,由互斥事件概率的加法公式,计算可得答案;
(2)分析题意,可得n≥2时,pn=
pn-1+
(1-pn)=
-
pn-1,类比数列的性质,可以构造等比数列{pn-
},求出其通项公式,进而可得答案.
(2)分析题意,可得n≥2时,pn=
| 1 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 15 |
| 9 |
| 19 |
解答:解:(1)根据题意,p2即第2次按下按键后出现红球的概率,
其包括第一次出现红球与绿球2种情况;
则p2=
×
+
×
=
.
(2)依题意,n≥2时,pn=
pn-1+
(1-pn)=
-
pn-1,
设常数λ∈R,使pn-λ=-
(pn-1-λ),即pn=
λ-
pn-1,解
λ=
得λ=
,
所以{pn-
}是首项为p1-
=
,公比为-
的等比数列,
所以pn-
=
×(-
)n-1,
解得pn=
[18+(-
)n-1].
其包括第一次出现红球与绿球2种情况;
则p2=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 7 |
| 15 |
(2)依题意,n≥2时,pn=
| 1 |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| 4 |
| 15 |
设常数λ∈R,使pn-λ=-
| 4 |
| 15 |
| 19 |
| 15 |
| 4 |
| 15 |
| 19 |
| 15 |
| 3 |
| 5 |
| 9 |
| 19 |
所以{pn-
| 9 |
| 19 |
| 9 |
| 19 |
| 1 |
| 38 |
| 4 |
| 15 |
所以pn-
| 9 |
| 19 |
| 1 |
| 38 |
| 4 |
| 15 |
解得pn=
| 1 |
| 38 |
| 4 |
| 15 |
点评:(2)有一定难度,要求学生将题中文字语言转化为符号语言,建立递推关系,通过适当“平移”将一次递推关系转化为等比关系,依据等比数列基本性质求解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 ,从按键第二按下起,若前次出现红球,则下一次出现红球、绿球的概率分别是
,从按键第二按下起,若前次出现红球,则下一次出现红球、绿球的概率分别是 、
、 ;若前次出现绿球,则下一次出现红球、绿球的概率分别是
;若前次出现绿球,则下一次出现红球、绿球的概率分别是 、
、 .记第n(n∈N*)次按下按键后出现红球的概率为pn.
.记第n(n∈N*)次按下按键后出现红球的概率为pn. ,从按键第二按下起,若前次出现红球,则下一次出现红球、绿球的概率分别是
,从按键第二按下起,若前次出现红球,则下一次出现红球、绿球的概率分别是 、
、 ;若前次出现绿球,则下一次出现红球、绿球的概率分别是
;若前次出现绿球,则下一次出现红球、绿球的概率分别是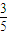 、
、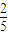 .记第n(n∈N*)次按下按键后出现红球的概率为pn.
.记第n(n∈N*)次按下按键后出现红球的概率为pn. ,从按键第二按下起,若前次出现红球,则下一次出现红球、绿球的概率分别是
,从按键第二按下起,若前次出现红球,则下一次出现红球、绿球的概率分别是 、
、 ;若前次出现绿球,则下一次出现红球、绿球的概率分别是
;若前次出现绿球,则下一次出现红球、绿球的概率分别是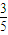 、
、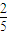 .记第n(n∈N*)次按下按键后出现红球的概率为pn.
.记第n(n∈N*)次按下按键后出现红球的概率为pn.