题目内容
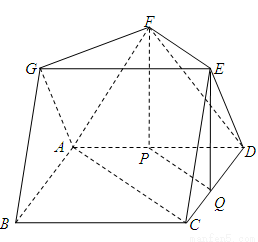
如图,在多面体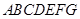 中,四边形
中,四边形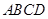 是边长为2的正方形,平面
是边长为2的正方形,平面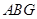 平面
平面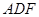 ,平面
,平面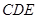 都与平面
都与平面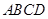 垂直,且
垂直,且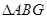 、
、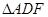 、
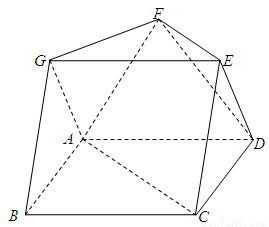
、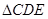 都是正三角形。
都是正三角形。
(1)求证: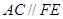 ;
;
(2)求多面体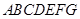 的体积。
的体积。
【答案】
(1)取 的中点,所以
的中点,所以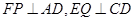 ,且
,且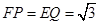 所以
所以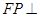 平面
平面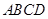 ,
,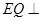 平面
平面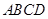 所以
所以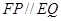 ,且
,且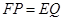 所以
所以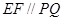 。因为
。因为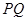 是
是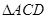 的中位线,所以
的中位线,所以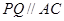 所以
所以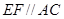 (2)
(2)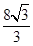
【解析】
试题分析:(1)如图,分别取 的中点
的中点
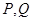 ,连接
,连接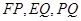
因为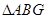 、
、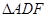 、
、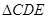 都是边长为2的正三角形
都是边长为2的正三角形
所以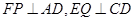 ,且
,且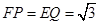
又因为平面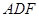 ,平面
,平面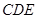 都与平面
都与平面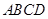 垂直
垂直
所以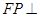 平面
平面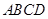 ,
,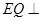 平面
平面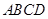
所以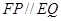 ,且
,且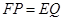
所以四边形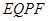 是平行四边形
是平行四边形
所以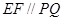 。因为
。因为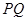 是
是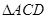 的中位线,所以
的中位线,所以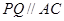
所以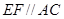
(2)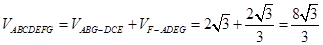
考点:线线,线面平行垂直的判定与性质及多面体体积
点评:在求证线线,线面位置关系时要用到基本的判定定理性质定理,要求对基本定理要理解熟记,在求解多面体体积时将其分解为椎体柱体等常见几何体再求其体积和

练习册系列答案
相关题目
 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:①3;②4; ③5;④6;⑤7.以上结论正确的为
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:①3;②4; ③5;④6;⑤7.以上结论正确的为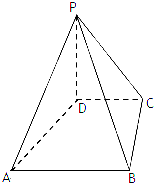 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.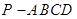 中,
中,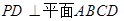 ,
,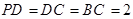 ,
, ,
,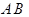 ∥
∥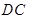 ,
,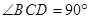 .
.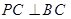 ;
;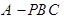 的体积.
的体积.
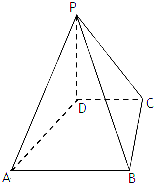 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=2,AB=2DC,AB∥DC,∠BCD=90°.