题目内容
13.已知二次函数f(x)=x2+2x-1(1)若奇函数h(x)的定义域和值域都是区间[-k,k],且x∈[-k,0],h(x)=-f(x)-1,求k的值;
(2)设函数g(x)=logt[f(x)-(t+2)x+2],其中0<t<2且t≠1.求证:恒存在实数p,q,r∈[0,1],使得g(p)+g(q)<g(r)成立.
分析 (1)由奇函数的定义可得h(x)的解析式,由于奇函数h(x)的定义域和值域都是区间[-k,k],则可令h(x)=±x,解得k=1和3,再加以检验即可得到k的值;
(2)运用对数函数的运算性质和单调性,结合题意,讨论0<t<1和1<t<2时,举出p,q,r的数值,即可判断是否存在.
解答 (1)解:x∈[-k,0],h(x)=-f(x)-1=-x2-2x,
令x∈[0,k],-x∈[-k,0],h(-x)=-x2+2x,
由奇函数h(x)可得h(-x)=-h(x),
即有h(x)=x2-2x(0≤x≤k),
综上可得,h(x)=x|x|-2x(-k≤x≤k),
由于奇函数h(x)的定义域和值域都是区间[-k,k],
则可令h(x)=±x,
由x|x|-2x=x,解得x=3(0舍去);
由x|x|-2x=-x,解得x=1(0舍去).
当k=1时,即有定义域和值域为[-1,1],
由y=x2-2x(0≤x≤1)可得值域为[-1,0];
由y=-x2-2x(-1≤x≤0)可得值域为[0,1],
则有h(x)的值域为[-1,1];
当k=3时,即有定义域和值域为[-3,3],
由y=x2-2x(0≤x≤3)可得值域为[-1,3];
由y=-x2-2x(-3≤x≤0)可得值域为[-3,1],
则有h(x)的值域为[-3,3];
综上可得,k=1或3;
(2)证明:函数g(x)=logt[f(x)-(t+2)x+2]
=logt(x2-tx+1)(0<t<2且t≠1),
由g(p)+g(q)<g(r)即为
logt(p2-tp+1)+logt(q2-tq+1)<logt(r2-tr+1),
即为logt[(p2-tp+1)(q2-tq+1)]<logt(r2-tr+1),
当1<t<2时,有(p2-tp+1)(q2-tq+1)<r2-tr+1,
即为(p2-p+1)(q2-q+1)<r2-r+1,且(p2-2p+1)(q2-2q+1)<r2-2r+1,
存在p=q=r=$\frac{1}{2}$,成立;
同样当0<t<1时,存在p=q=$\frac{1}{2}$,r=$\frac{7}{8}$使得g(p)+g(q)<g(r)成立.
故有恒存在实数p,q,r∈[0,1],使得g(p)+g(q)<g(r)成立.
点评 本题考查函数的性质和运用,主要考查函数的奇偶性和值域的求法,同时考查存在性命题的证明,注意运用列举法的运用,属于中档题和易错题.

 矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF展开后再折成如图所示,使点A落在EF上的点A′处,求第二次折痕BG的长.
矩形ABCD中,AB=6,BC=8,先把它对折,折痕为EF展开后再折成如图所示,使点A落在EF上的点A′处,求第二次折痕BG的长.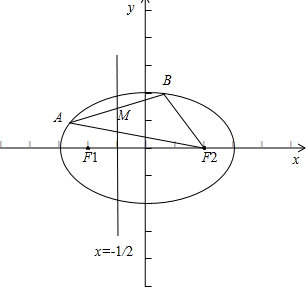 如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.
如图,F1,F2是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左、右焦点,A,B是椭圆C上的两个动点,且线段AB的中点M在直线l:x=-$\frac{1}{2}$上.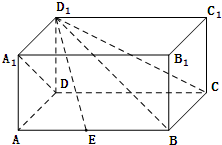 在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.
在四棱柱ABCD-A1B1C1D1中,侧棱DD1⊥底面ABCD,底面ABCD是矩形,且AD=AA1.
 如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证:
如图,正方体ABCD-A1B1C1D1中,E,F分别是AB,BC的中点.求证: