题目内容
已知曲线W上的动点M到点F(1,0)的距离等于它到直线x=-1的距离.过点P(-1,0)任作一条直线l与曲线W交于不同的两点A、B,点A关于x轴的对称点为C.(1)求曲线W的方程;
(2)求证:![]() =λ
=λ![]() (λ∈R);
(λ∈R);
(3)求△PBC面积S的取值范围.
答案:(1)解:由题知,曲线W是以F(1,0)为焦点,以直线x=-1为准线的抛物线,
所以曲线W的方程为y2=4x.
(2)证明:因为直线l与曲线W交于A、B两点,所以l的斜率k存在,且k≠0,
设直线l的方程为y=k(x+1),由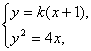 得k2x2+(2k2-4)x+k2=0.
得k2x2+(2k2-4)x+k2=0.
因为直线l与曲线W交于A、B两点,

所以k≠0,Δ=4(k2-2)2-4k4>0,即|k|<1且k≠0.
设点A,B的坐标分别为(x1,y1),(x2,y2),
则x1+x2=![]() ,x1x2=1,点C的坐标为(x1,-y1),
,x1x2=1,点C的坐标为(x1,-y1),
y1=k(x1+1),y2=k(x2+1).
所以![]() =(x1-1,-y1),
=(x1-1,-y1),![]() =(x2-1,y2).
=(x2-1,y2).
又因为(x1-1)y2-(x2-1)(-y1)=(x1-1)k(x2+1)+(x2-1)k(x1+1)=k(2x1x2-2)=0,
所以![]() =λ
=λ![]() .
.
(3)由题意S=![]() |PF|·|y1+y2|
|PF|·|y1+y2|
=|k(x1+x2+2)|=|k(![]() +2)|=
+2)|=![]() .
.
因为|k|<1且k≠0,所以S的取值范围是(4,+∞).

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 ,向量
,向量 .
. 的特征值
的特征值 、
、 和特征向量
和特征向量 ;
; 的值.
的值. .以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 .
. ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m  ;
;